1) compact metric space
紧致度量空间
1.
Transitivity and chaos of a sequence of maps in a compact metric space;
紧致度量空间中一列映射的传递性和混沌性
2.
A further fixed point theorem was proved for mappings satisfying implicit relation functions on two compact metric spaces.
首先给出了隐含关系函数,证明了满足隐含关系函数的两个映射的公共不动点定理,进一步证明了两个紧致度量空间上满足隐含关系函数的不动点定理。
3.
Finally,as to an equicontinuous homeomorphism on a compact metric space,from the minimality and compactness of the space,a finite subcover is acquired,which is formed by open neighborhoods centered at the finite-lengthed orbits of some finite points with radius ε2.
最后,针对紧致度量空间上的等度连续同胚,利用空间的极小性和紧致性,得到以空间中某有限个点的有限长轨道为中心,以ε2为半径的开邻域构成的有限子覆盖,并利用f的等度连续性,由该子覆盖构造出以空间任一点的有限长轨道为中心的开邻域所作成的有限子覆盖,进而得到所要结论。
3) Compact metric space
紧度量空间
1.
The fixed point theorem of contraction maps is established,an example about that contraction maps have not fixed point in a completment metric space is given,and approach theorem of fixed point of contraction maps in compact metric spaces is obtained.
建立了收缩映射的不动点定理 ,给出了完备度量空间中没有不动点的收缩映射的例子 ,并讨论了紧度量空间中收缩映射不动点的迭代逼近问
2.
The present paper proves that the continuous map of a compact metric space is the sufficient condition of distributional chaos in a squence.
给出紧度量空间上连续映射按序列分布混沌的一个充分条件，并证明区间连续自映射是混沌的当且仅当它是按某序列分布混沌
4) compact space
紧致空间
1.
In this paper,the Cartesian Product of three topological spaces,compact space,connected space and A2(A1) space,were studied,and three corresponding conclusions are given.
讨论了某些拓扑空间的有限笛卡儿乘积,主要包括紧致空间、连通空间、以及A2(A1)空间。
5) locally compact metric spaces
局部紧度量空间
1.
Closed images of locally compact metric spaces;
局部紧度量空间的闭映象
6) precompact metric space
准紧度量空间
补充资料：度量空间
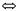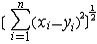| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…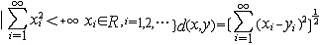）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条