1) second order parabolic equation


二阶抛物方程
1.
In this paper,anisotropic nonconforming rectangular finite element approximation to the second order parabolic equations is studied.
讨论了各向异性非协调矩形元对二阶抛物方程的逼近,利用该单元的特殊性质及新的技巧,在各向异性网格下得到了与传统有限元方法完全相同的最优的误差估计。
2.
In this paper,anisotropic nonconforming rotated Q1 element approximation to the second order parabolic equation on square meshes is discussed.
在正方形网格上讨论了非协调旋转Q1元对二阶抛物方程的逼近。
2) two-order parabolic equation


二阶抛物型方程
1.
A family of high-accurate and three-layer difference schemes containing parameters are constructed for solving two-order parabolic equation.
对二阶抛物型方程构造了一族含参数高精度三层差分格式。
3) Second order linear parabolic equation


二阶线性抛物型方程
1.
To the second order linear parabolic equation with independent variables au_(xx)+2bu_(xy)+cu_(yy)+du_x+eu_y+g=0 when its coefficients satisfy given conditions,we may utilize the transformation T:ξ=φ(x,y);η=x to make it as first order linear ordinary differential equation for solving.
二个自变量的二阶线性抛物型方程auxx+2buxy+cuyy+dux+euy+g=0,当系数满足一定条件时,可以利用变换T:ξ=φ(x,y);η=x化为一阶线性常微分方程求解,该文给出了判别定理和应用方法。
4) degenerate parabolic equations of second order


二阶退化抛物型方程
1.
The asymptotic behavior of a sort of degenerate parabolic equations of second order;


一类具有散度头部的二阶退化抛物型方程解的渐近性态
6) second-order parabolic system


二阶抛物型方程组
1.
In Chapter One,a new method of approximating the solution of second-order parabolic system using reproducing kernel function is devised.
第一章研究了一类二阶抛物型方程组的一种新数值方法-再生核函数法。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 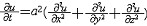 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式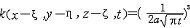 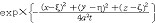 热传导方程初值问题的解可用基本解叠加而成,即 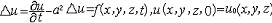 的解为 的解为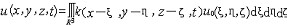 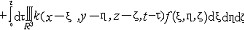 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 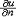 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条