1) divisor of algebraic number field
代数数域的除子
2) divisor of algebraic function field
代数函数域的除子
3) divisor of algebraic variety
代数簇的除子
4) divisor of algebraic curve
代数曲线的除子
5) L-subalgebras over L-subfields
L子域上的L子代数
6) TL-subalgebras over TL-subfields
TL-子域上的TL-子代数
1.
TL-subalgebras over TL-subfields;
TL-子域上的TL-子代数
补充资料：代数数
| 代数数 algebraic number 满足形如anxn＋an-1xn-1＋…＋a1x＋a0＝0（n≥1，an≠0）的某整系数代数方程的实数或复数。例如 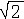 是一个实代数数，它满足方程x2－2＝0。每个有理数 （m，n为整数，n≠0）都是代数数，因为它满足方程nx-m ＝0。可见代数数集包含了有理数集。然而，代数数集并不包含全部实数。代数数集是一个可数集，即所有代数数能与全体自然数建立一一对应，而实数集是不可数的无穷集，因此，一定存在不是代数数的实数。现已证明 π和e这些无理数不是代数数。不是代数数的数称为超越数。由此可见，就实数集而言，实数既可按有理数和无理数分为两类，又可按实代数数和实超越数分为两类。实代数数集是有理数集的自然扩充。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条