1) arithmetic of algebraic number fields
代数数域的数论
2) arithmetic of algebras
代数的数论
3) algebraic number field
代数数域
4) divisor of algebraic number field
代数数域的除子
5) genus of algebraic number field
代数数域的亏格
6) algebraic number theory
代数数论
1.
By using congruence theory and algebraic number theory,proved that the Diophantine equation x 2 + 1 =y5 has only integer solution(x,y)=(0,1)and the Diophantine equation x 2 + 64 =y3 has no integer solution.
利用同余理论和代数数论的有关结论,证明了不定方程x2+1=y5仅有整数解(0,1)以及不定方程x 2+64=y3无整数解。
补充资料：代数数
| 代数数 algebraic number 满足形如anxn＋an-1xn-1＋…＋a1x＋a0＝0（n≥1，an≠0）的某整系数代数方程的实数或复数。例如 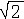 是一个实代数数，它满足方程x2－2＝0。每个有理数 （m，n为整数，n≠0）都是代数数，因为它满足方程nx-m ＝0。可见代数数集包含了有理数集。然而，代数数集并不包含全部实数。代数数集是一个可数集，即所有代数数能与全体自然数建立一一对应，而实数集是不可数的无穷集，因此，一定存在不是代数数的实数。现已证明 π和e这些无理数不是代数数。不是代数数的数称为超越数。由此可见，就实数集而言，实数既可按有理数和无理数分为两类，又可按实代数数和实超越数分为两类。实代数数集是有理数集的自然扩充。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条