1) Lebesgue convepgence


勒贝格收敛
2) Lebesgue control constringency theroem


勒贝格控制收敛定理
3) Lebesgue


勒贝格
1.
Creative Thoughtway and Mathematical Discovery of Lebesgue;


勒贝格的数学发现与创造性思想方法
4) lebesgue number


勒贝格数
5) Henri Léon Lebesgue (1875~1941)


勒贝格,H.L.
6) lattice-convergence


格收敛
1.
The properties of the l*-topology and l*-topological group have been discussed, according to the lattice-convergence defined on the basis of a double lattice ordered algebraic structure l* -module in this paper.
基于在双格序代数结构l*-模上定义的格收敛概念,讨论产l*-拓扑和l&-拓扑群的性质。
补充资料:勒贝格积分
| 勒贝格积分 Lebesgue integral 分析数学中普遍使用的工具。1902年由法国数学家H.L.勒贝格建立。它是黎曼积分(简记为(R)积分)的重要推广,它克服了(R)积分的许多局限性。一个在[a,b]上(R)可积的有界函数一定在[a,b]上勒贝格可积〔简记为(L)可积〕,但反之不然。典型的例子是狄利克雷函数D(x),它在[0,1]中的有理数上取值为1,在其余点取值为0,则D(x)在[0,1]上有界,(R)不可积,但(L)是可积的,积分值为0。 (L)积分除了具有与(R)积分相似的性质(例如线性性质、对积分区域的有限可加性、单调性等)外,还有其特有的性质:对积分区域的可列可加性、唯一性、绝对可积性、绝对连续性,以及有关交换积分与极限次序的三大定理:单调收敛定理、法都引理、勒贝格控制收敛定理等。正是这些基本性质使得(L)积分具有广泛的应用。例如:利用单调收敛定理及(L)积分与(R)积分间的关系,可以很容易地进行逐项积分,得到 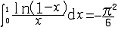
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |