1) Nondivergent parabolic equations


非散度型抛物方程
2) non-divergence quasilinear parabolic equation


非散度型拟线性抛物型方程
1.
The existence of classical solutions to non-divergence quasilinear parabolic equation of second order has been proved by basic knowledge of non-linear functional analysis and implicit function theorem in banach spaces.
用非线性泛涵分析的基本知识和Banach空间上的隐函数定理证明了非散度型拟线性抛物型方程古典解的存在性。
4) non linear parabolic equations/reaction diffusion systems


非线性抛物型方程/反应扩散系统
5) coupled parabolic equation dispersion problem


耦合型抛物方程弥散项
6) parabolic reaction-diffusionequation


抛物型反应-扩散方程
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 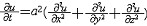 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式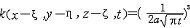 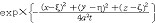 热传导方程初值问题的解可用基本解叠加而成,即 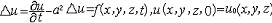 的解为 的解为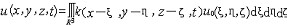 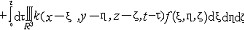 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 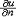 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条