1) nonlocal parabolic system


非局部抛物型方程组
2) nonlocal parabolic equation


非局部抛物型方程
1.
In this paper,the Schauder fixed point theorem is used to deal with the existence and uniqueness of solutions for a class of nonlocal parabolic equations.
利用Schauder不动点定理讨论了一类非局部抛物型方程解的存在性及唯一性。
3) nonlinear parabolic equations


非线性抛物型方程组
1.
Global existence and blow up for a nonlinear parabolic equations;


一类非线性抛物型方程组解的整体存在及爆破
2.
Global existence and blow up problem for a nonlinear parabolic equations


一类非线性抛物型方程组解的整体存在及爆破问题
3.
A study is made on the blowing up problem for the nonlinear parabolic equations u t=Δu m,v t=Δv m, m≥1,with nonlinear boundary conditions u n=u p·v q, v n=u r·v s.
研究了带非线性边界条件 u n =up·vq, u n=ur·vs的非线性抛物型方程组ut =Δum,vt =Δvm(m ≥1)时的爆破问题 。
4) nonlinear parabolic systems


非线性抛物型方程组
1.
Based on triangular meshes, we present a finite volume element framework for a class of two dimensional nonlinear parabolic systems.
讨论基于三角形网格的二维非线性抛物型方程组的有限体积元方法,其中试探函数空间为二次Lagrange元,检验函数空间为分片常数函数空间,对问题的全离散格式证明了最优的能量模误差估计。
2.
The initial regular oblique derivative problem for nonlinear parabolic systems of several second order complex equations with measurable coefficients in a multiply connected domain is discussed.
论述了多连通区域上可测系数的二阶非线性抛物型方程组的初-正则斜微商问题。
5) Nonlinear parabolic system


非线性抛物型方程组
1.
Galerkin alternating-direction procedures are considered for the nonlinear parabolic systems q i(ξ,u)u it-∑kj=1·(a~ ij (ξ,u)u j)+∑kj=1 b~ → ij (ξ,u)·u j=f i(ξ,t,u),1≤i≤k.
利用等参变换、在局部有限单元上近似Jacobi行列式p(x)及系数qi(ξ,u),1≤i≤k等方法,对非矩形区域上非线性抛物型方程组qi(ξ,u)uit-∑kj=1·(a~ij(ξ,u)uj)+∑kj=1b~→ij(ξ,u)·uj=fi(ξ,t,u),1≤i≤k,提出了一类方向交替Galerkin格式,并得到最优的L2-和H1-误差估计。
6) nonlocal elliptic system


非局部椭圆型方程组
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 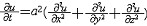 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式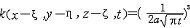 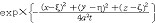 热传导方程初值问题的解可用基本解叠加而成,即 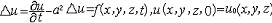 的解为 的解为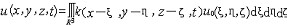 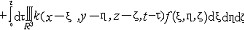 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 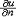 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条