1) complex harmonic function


复调和函数
1.
The mixed boundary value problems for complex harmonic functions;


复调和函数的混合边值问题
2.
Cauchy integral formula for complex harmonic functions;


复调和函数的Cauchy积分公式
3.
In this paper, the properties of complex harmonic function on infinity are considered , and the relationship between two kinds of expressions of complex harmonic function is discovered.
本文讨论了复调和函数在无穷远点的性质,揭示出有界区域上复调和函数的两类表示式之间的关系。
2) compound harmonic function


复谐函数,复调和函数
3) univalent compound harmonic functions


单叶复调和函数
4) complex hyperharmonic function


复超调和函数
1.
In the first part of this paper,resorting to the idea of quasi-permutation which created by Sha Hang,we give the equivalent conditions of complex monogenic and complex hypermonogenic functions,define the complex hyperharmonic function and discuss its equivalent conditions.
第一部分借助黄沙老师拟置换的思想,得到了复正则函数,复超正则函数的等价条件,定义了复超调和函数并讨论了它的等价条件,第二部分讨论了复超正则函数的若干性质。
5) complex valued harmonic conjugate function


共轭复调和函数
1.
In this paper, complex valued harmonic conjugate function is defined, Cauchy Riemann equations of complex valued harmonic functions are considered.
定义了复调和函数的共轭复调和函数,给出了复调和函数的Cauchy—Rie-mann方程,同时讨论了它们与解析函数之间的关
6) harmonic function


调和函数
1.
Integral Representation and Estimation of Harmonic Functions in Half-Plane;


半平面中调和函数的积分表示和估计
2.
The Dirichlet boundary value problem for harmonic function;


调和函数的Dirichlet边值问题
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 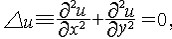 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有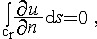 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,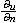 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在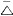 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: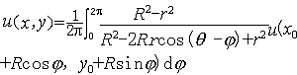
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |