1) subharmonic function


次调和函数
1.
In this paper,we mainly study the property of subharmonic function on strongly symmetric manifolds with a pole,and prove that if the Ricci curvature satisfies some decaying conditions,the mean value of the Laplacian operator of any subharmonic function decays faster than quadratically,then this function must be harmonic.
主要通过研究强对称流形上的次调和函数的性质,证明了在带有极点的强对称流形上,若它的Ricci曲率满足一定的衰竭条件,且对任一次调和函数的Laplace算子的平均值衰竭的比平方快,则此函数是调和的。
2.
In the second chapter,we give some definition and basic theorem,such as Hilbert-Schmidt operator,essential norm,compact operator and some properties of subharmonic function.
第二章主要给出了一些相关的定义和基本的定理,主要有Hilbert-Schmidt算子,本性范数,紧算子和次调和函数的一些性质等。
3) superior subharmonic function


上次调和函数
1.
It is brought forward superior subharmonic function,which is between harmonic function and analytic function.
本文提出了一类介于解析函数和调和函数之间的函数,称为上次调和函数,并且讨论了上次调和函数的一些性质和特征。
4) strongly pluriharmonic function


强多次调和函数
5) plurisubharmonic functions


多次调和函数
1.
This is a survey of results, both classical and recent, on behaviour of plurisubharmonic functions, together with the related topic for positive closed currents.
这篇文章主要是对复几何与复流形中的多次调和函数的性质及其应用作一综述。
6) plurisubharmonic function


多重次调和函数
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 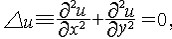 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有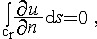 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,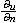 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在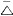 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: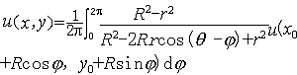
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |