1) biharmonic function


双调和函数
1.
A representation for the velocity and pressure fields in three dimensional Stokes flow was presented in terms of a biharmonic function A and a harmonic function B.
利用双调和函数A和调和函数B,给出了三维Stokes流动速度场和压力场的描述· 由此建立了计算区域边界为固定无滑移平面边界Stokes流动基本奇异性的一般定理· 刚性平面前轴对称Stokes流动的Collins定理成为本文定理的特例· 给出的几个例证说明了方法的有效性·
2.
The converse theorems of mean value theorem of two and three dimensional biharmonic function are presented and prove
提出并证明了二维和三维双调和函数中值定理的逆定
2) biharmonic functions


双调和函数
1.
By investigating the relations of bianalytic functions and biharmonic functions, the uniqueness and existence of the stress functions (Airy functions) are established in planar simple connected region.
通过考虑双解析函数和双调和函数的关系 ,对单连通区域上平面弹性问题中只有重力体力作用的应力函数建立了唯一性和存在性结果 ;并对单位圆区域得到了类似于Poisson公式解的积分表示式
2.
The boundary value problem for biharmonic functions appeared in the bending of clamped thin plate is considered.
一类双调和函数的边值问题路见可武汉大学数学系,430072,武汉关键词弹性薄板,双调和函数,全纯函数分类号(中图)O175。
3) biharmonic Green function


双调和Green函数
1.
In this paper,the biharmonic Green function Г(z,w) is studied.


我们得到了双调和Green函数的一些性质 ,并由此指出ZhuKehe的有关双调和Green函数的几个结果是错误
4) hyperbolically harmonic functions


双曲调和函数
1.
A nonlinear boundary value problem for hyperbolically harmonic functions in the Clifford analysis;
Clifford分析中双曲调和函数的非线性边值问题
2.
Discuss the representation of hyperbolically harmonic functions associated to the harmanic functions that have known in Clifford analysis.
讨论Cliford分析中给定一个调和函数得出相应双曲调和函数的表达式,并给出2个问题解的存在唯一性和积分表达
3.
In this paper,we discuss the integral representation of hyperbolically harmonic functions in the Clifford analysis, and gives the existence of solution of a kind of boundary value problem for hyperbolically harmonic functions.
本文讨论Clifford分析中双曲调和函数的积分表达式及其一种边值问题解的存在性。
5) biharmonic spline interpolation


双调和样条函数
1.
Image mapping approach based on biharmonic spline interpolation concerning dot arrangement and multi-mapping
针对在DSPIV(Digital Stereo Particle Image Velocimetry)的图像几何校正中,校正板上控制点的排列方式对图像校正误差所产生的影响,在使用双调和样条函数构建校正映射函数的条件下,分别使用了11列×21行、21列×21行、11列×41行、21列×41行和16列×31行5种控制点等列距、等行距排列的校正板来进行图像校正,计算了这5种控制点排列方式对应的校正准度和校正精度。
6) harmonic function


调和函数
1.
Integral Representation and Estimation of Harmonic Functions in Half-Plane;


半平面中调和函数的积分表示和估计
2.
The Dirichlet boundary value problem for harmonic function;


调和函数的Dirichlet边值问题
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 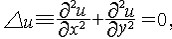 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有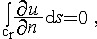 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,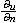 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在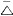 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: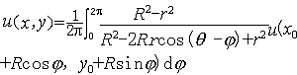
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |