1) germ of harmonic function


调和函数芽
2) harmonic function


调和函数
1.
Integral Representation and Estimation of Harmonic Functions in Half-Plane;


半平面中调和函数的积分表示和估计
2.
The Dirichlet boundary value problem for harmonic function;


调和函数的Dirichlet边值问题
3) A-harmonic functions


A-调和函数
1.
Then,we further obtain that each bounded weak solution is of sharp Hlder exponent with anyγ:0≤γ<k under the additional data regularity assumptions,where k is just as the local Hlder index of A-harmonic functions.
利用Moser-Nash迭代和稠密引理,得到了在自然增长下的非线性退化椭圆方程有界弱解具有某一Hlder指数的正则性;在已知数据的进一步正则性下,建立了具有任意γ满足0≤γ<κ的优化Hlder连续性指数,其中κ是A-调和函数的局部Hlder连续指数。
4) harmonic functions


调和函数
1.
karp to prove that on such kind of 2 Mfd which curvature k≥-1r 2 log r outside a compact set there exist no nonconstant subharmonic functions which bounded f.
Karp的方法证明:在某个紧致集外满足曲率k≥-1r2logr的二维流形上不存在有上界的非常值下调和函数。
2.
In this paper, applying Life theory of complex-functional, not only the space harmonic functions in polynomial form but also the spherical functions are obtained.
本文以泛复变函数为工具,成功地构造出多项式型空间调和函数族,通过坐标变换和正交化过程,进而又获得了球函数。
3.
It is proved for harmonic functions an integral identity.


本文推导出调和函数的一个积分恒等式,并把这个结果推广到方程△_pu=0(P>1)的解的情形。
5) harmonic functions


拟调和函数
1.
The basic equations are generalized from those of the transversely isotropic magneto-electro-elastic media, and the general solutions in forms of harmonic functions in the case of distinct eigenvalues are derived.
从横观各向同性磁电弹性体的三维基本方程出发,简化得到平面问题的基本方程,给出了用4个拟调和函数表达的4个特征根互异情况下的通解,进而以试凑法推导出了自由端作用集中力的悬臂磁电弹性梁的位移、电势、磁势、应力、电位移和磁通密强度的解析解,所得解易于理解、便于校对、形式简洁。
2.
The basic equations are generalized from those of the transversely isotropic magnetoelectroelastic media, and the general solution in forms of harmonic functions in the case of distinct eigenvalues are derived.
从横观各向同性磁电弹性体的三维基本方程出发,简化得到平面问题的基本方程,给出了用四个拟调和函数表达的四个特征根互异情况下的通解,进而以试凑法推导出了均布荷载作用下简支磁电弹性梁的位移、电势、磁势、应力、电位移和磁通密强度的解析解,所得解有易于理解、便于校对、形式统一简洁的特点。
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 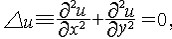 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有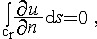 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,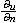 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在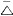 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: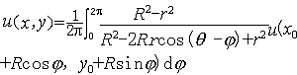
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |