1) k-hyperbolically harmonic function


k-超调和函数
1.
A partial differential equations is introduced on the basis of the definitions of k-hypermonogenic function with vector value and the k-hyperbolically harmonic function,then the porperties of k-hypermonogenic function with vector value and their relations are discussed,at last a sufficient and necessary condition for the solvability of partial differential equations is obtained.
在k-超正则向量值函数和k-超调和函数定义的基础上,引入了一个偏微分方程组,然后借助这个偏微分方程组讨论了k-超正则向量值函数的性质及其与k-超调和函数的关系,最后给出了偏微分方程组可解的一个充分必要条件。
2) k-harmonic function


k调和函数
1.
Moreover, it is also proved that solutions of the Dirichlet boundary value problems for above two classes of functions and the k-harmonic function uniquely exist.
讨论了k 正则函数的若干函数论性质和获得了非齐次k阶方程 k zku =f的积分形式的特解 ,证明了以上两类函数及k调和函数的Dirichlet边值问题的解是存在唯一的 。
3) K-harmonic functions


K-调和函数
1.
On the basis of the defination of K-integral,this essay deducts out the relation between K-analytic function and K-integral and the relation between K-analytic function and K-harmonic functions.
在定义了K-积分的基础上,给出了K-解析函数与K-积分、K-调和函数的关系,所得结论是解析函数与共轭解析函数中相应结果的继续和应用。
4) hyperharmonic function


超调和函数
5) complex hyperharmonic function


复超调和函数
1.
In the first part of this paper,resorting to the idea of quasi-permutation which created by Sha Hang,we give the equivalent conditions of complex monogenic and complex hypermonogenic functions,define the complex hyperharmonic function and discuss its equivalent conditions.
第一部分借助黄沙老师拟置换的思想,得到了复正则函数,复超正则函数的等价条件,定义了复超调和函数并讨论了它的等价条件,第二部分讨论了复超正则函数的若干性质。
6) Super space time harmonic function


超空时调和函数
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 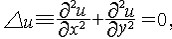 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有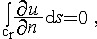 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,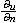 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在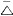 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: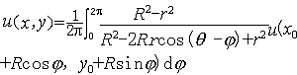
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |