1)  partial differential equation
偏微分方程
1.
Forced oscillation for solutions of systems of high order nonlinear neutral type partial differential equations with delays;
高阶非线性中立型时滞偏微分方程系统解的强迫振动性
2.
Using of the partial differential equation in working holes of boxes;
偏微分方程在箱体孔系加工中的应用
3.
A forth-order partial differential equation used for image denoising;
用于图像去噪的一个四阶偏微分方程
2)  partial differential equation
偏微分方程组
1.
The paper rewrites the traffic flow macro models in the form of system of quasilinear hyperbolic partial differential equation of first order, and classifies the models in terms of the coefficient in the equation.
将交通流模型表示成拟线性一阶双曲型偏微分方程组;按照方程组中的系数值,对交通流的各种宏观模型进行了分类;依据特征线的特征速度是否小于宏观运动速度,模型是否依赖外来的速度-密度平衡关系以及模型代表的交通流特点等三项指标对模型进行了评价。
2.
Existence and uniqueness of local analytic solution of the partial differential equations |k i| ux k i =A i(x,u,.
把柯西 -柯尔列夫斯卡娅定理推广到如下偏微分方程组 : | ki| u xki =Ai( x,u,… , |α| u xα )( i =1,… ,r, x =( x1 ,… ,xm) ,|α| =α1 +… +αm) 。
3)  partial differential equation
微分方程式
4)  nonlinear partial differential equation
非线性偏微分方程
1.
Classification of Bcklund transformations among second-order nonlinear partial differential equations;
二阶非线性偏微分方程之间Bcklund变换的分类
2.
Based on the Homogeneous Balance Method,four methods to find exact traveling wave solutions of nonlinear partial differential equations are proposed by using trigonometric functions,hyperbolic functions and Mathematica software.
基于齐次平衡法的思想,借助数学软件"Mathematia",利用三角函数、双曲函数和吴消元法建立了四种寻找非线性偏微分方程行波解的方法,方法的基本原理是通过一些特殊的变换,将求方程行波解的问题转化为求代数方程的解问题,并且以复合KdV方程作为例子,介绍了方法及其步骤。
3.
By utilizing the trial function method, a class of nonlinear partial differential equations (PDEs for short) that are hard to be solved by the usual ways can be reduced to a set of algebraic equations, which can be easily solved, and their related coefficients can be easily determined by the undetermined coefficients method.
利用试探函数法,将一个难于求解的非线性偏微分方程化为一个易于求解的代数方程,然后用待定系数法确定相应的常数,简洁地求得了一类非线性偏微分方程的精确解。
5)  discrete partial differential equation
离散PDE
6)  vector partial differential equation
矢量偏微分方程
1.
The corresponding Green s function equation of a vector partial differential equation is splitted into irrotational and solenoidal part.
将一类矢量偏微分方程相对应的并矢格林函数方程分解成无旋和无散部分 ,给出推导一类场矢量的并矢格林函数无旋和无散分解式的新方
参考词条
补充资料：偏微分方程
偏微分方程
partial differential equation

   含有未知函数及其各阶偏导数的方程。如(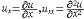!!!P0353_1余类此）
   ut－a2（uxx＋uyy＋uzz）＝0（1）其中u＝u（x，y，z，t）为未知函数，x，y，z，t是自变量。18世纪，数学家们已开始用偏微分方程来研究问题。方程（1）便是用来描述热的传导规律的。1746年，J.LeR.达朗贝尔给出了一维波动方程（两端固定的弦的振动问题）：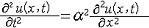
   !!!P0353_2由于弦的两端固定，故在x＝0和x＝l处（l为弦的长度）应满足边界条件：
   u（0，t）＝0   u（l，t）＝0
    t≥0（3）又当t＝0时的状态，即初始条件是
   u（0，x）＝j（x）  ut（0，x）＝ψ（x）（4）
   一般，每个偏微分方程有许多解，且含有任意函数，一阶方程的解含有一个任意函数，二阶方程的解含有两个任意函数，例如（2）有解u＝f（x－at）＋g（x＋at），其中f（x）、g（η）是二次可微的函数。通常，更注重求满足某些附加条件的特解：未知函数在初始时刻所满足的条件叫初始条件  ，如（4），在所给区域边界上所满足的条件叫边界条件，如（3），初始条件和边界条件统称定解条件，这都要由实际问题来确定。求方程满足初始条件的定解问题叫初值问题或柯西问题，只含边界条件的定解问题叫边值问题，既有初始条件，又有边界条件的问题称为初边值问题或混合问题。如果某个解，当定解条件中的量变化不大时，解的变化也不大，就称解连续依赖于定解条件。若定解问题的解存在、唯一且连续依赖于定解条件，就称定解问题为适定的或称问题的提法是正确的。
说明：补充资料仅用于学习参考，请勿用于其它任何用途。