1) Fermat Number
费马数
1.
An Algorithm for Multi-dimensional Fermat Number Transform;
多维费马数变换的一种算法
2.
Presents the study of second order linear constant coefficient progressive regression equation with the latest achievements in the “greatest common divisor” theory to give the great significance of Fibonacci combination series equation, Fermat Number, and Mersenne Number, and a only exceptional value each.
用“最大公约数”理论的最新结果 ,研究二阶线性常系数齐次递归方程 ,给出斐波那契数列组合式、费马数、梅森数在组合数学上的重要意义和它各自有一个且唯一例外
3.
In this paper we proved that a Fermat number is not part of a amicable triple.
对于不相同的正整数a,b,c,若σ(a)=σ(b)=σ(c)=a+b+c,则称它们为亲和三数组,在此给出了费马数不与任何正整数构成亲和三数组的结论。
2) Fermat numbers
费马数
1.
An application of Fermat numbers in the study of group theory;
费马数在群论研究中的一个应用
3) Fermat primes
费马素数
4) Fermat prime number
费尔马素数
5) generalized Fermat number
广义费马数
1.
A conclusion of generalized Fermat numbers
关于广义费马数的一个结论
6) Fermat type functional equations
费尔马函数方程
补充资料：费马数
| 费马数 Fermat number 形如 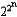 ＋1的正整数，记为Fn。由于已知F0＝3 ，F1＝5，F2＝17，F3＝257，F4＝65537都是素数，1640年，P.de费马曾猜想 ，一切费马数都是素数 。1732年L. 欧拉指 出 F5＝641 ×6700417 不是素数 。那么究竟有多少个费马数是素数？是有限个还是无限个？这是数论中未解决的难题之一。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条