1) power series


幂级数
1.
A proof to the analysis property of sumfaction of power series;


幂级数和函数分析性质的一种证明
2.
Elucidation about convergence radius of the sum of two power series;


关于2个幂级数和的收敛半径的说明
3.
A survey of solutions of sum functions of power series;


幂级数和函数的解法综述
2) power series method


幂级数法
1.
The prediction of the PIM amplitude and power by using the power series method;


幂级数法对无源交调幅度和功率的预测
2.
The natural frequencies and critical flow velocities of Timoshenko pipe are calculated by power series method.
用幂级数法计算了Tim oshenko 管道的固有频率和临界流速。
3.
Based on the Hamilton s principle for elastic systems of changing mass, a differential equation of motion for viscoelastic curved pipes conveying fluid was derived using variational method, and the complex characteristic equation for the viscoelastic circular pipe conveying fluid was obtained by normalized power series method.
根据变质量弹性系统Hamilton原理,用变分法建立了输流粘弹性曲管的运动微分方程,并用归一化幂级数法导出了输流粘弹性曲管的复特征方程组· 以两端固支Kelvin_Voigt模型粘弹性输流圆管为例,分析了无量纲延滞时间和质量比对输流管道无量纲复频率和无量纲流速之间的变化关系的影响· 在无量纲延滞时间较大时,粘弹性输流圆管的特点是它的第1、2、3阶模态不再耦合,而是在第1、第2阶上先发散失稳,然后在1阶模态上再发生单一模态颤振·
3) fuzzy power series expansion


Fuzzy幂级数
1.
In this paper, the authors define the fuzzy power series expansion and discuss the fuzzy function expanding into fuzzy power series, moreover, the fuzzy power series expansion of a class of type LR fuzzy function is given.
引入一类Fuzzy幂级数 ,讨论了Fuzzy函数的Fuzzy幂级数的展开 ,进而讨论了一类LR型Fuzzy函数的展开。
4) Negative exponent power series


负幂级数
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 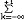 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有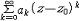 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数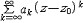 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形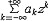 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条