1) power series expansion


幂级数展开
1.
Based on the theory of modal superposition and power series expansion, a modal superposition method for the sensitivity analysis of FRF is proposed in this paper.
基于模态展开和幂级数展开原理,提出了一种频响函数灵敏度分析的模态展开法。
2.
Based on the modal superposition and power series expansion when the considered eigenvectors lie in the middle frequency range,the high and low modal can be truncated at the same time.
特征值与特征向量灵敏度分析在振动控制、结构动力优化设计等邻域中有有着广泛的应用本文根据模态展开和幂级数展开原理,导出了一种可用于特征向量组灵敏度分析的幂级数展开法当所考察的特征向量组处于系统的低频区时,应用该方法可对系统中、高阶模态实施模态截断和加速;而当所考察的特征向量组处于系统的中频区时,应用该方法可对系统的高阶模态和低阶模态同时实施截断和加速数值示例计算表明,本文提出的方法是可行的
3.
The method of the power series expansion for Abelian integral by Mathematica program is used to prove that there are two limit cycles with arbitrary location.
采用将Abel积分进行幂级数展开的方法,借助于Mathematica编程计算,证明了其Poincaré分支可以产生位置具有任意性的两个极限环。
2) Taylor expansion


幂级数展开
1.
Making use of derivative rule of complex functions,how to compute a foot point latitude in ellipsoidal geodesy by Taylor expansion is described.
针对子午线弧长反解计算过于繁琐的问题,利用复合函数的求导法则,变换变量进行幂级数展开,给出了通项公式,利用Hermite插值原理推导了各参数,借助Mathematica计算机代数系统,得出了这些公式用偏心率e表示的幂级数表达式。
5) formal power series expansions


形式幂级数展开
6) expansion in powers of complex frequency


复频率幂级数展开
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 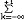 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有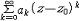 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数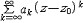 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形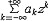 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条