1) kernel of a linear transformation
线性变换的核
3) image of linear transformtion
线性变换的象
5) linear transformation
线性变换
1.
On linear transformation and related results of matrix pade type approximation;
关于矩阵Padē—型逼近的一个线性变换及有关结果
2.
Derivation of Lorentz Transformation by Linear Transformation Method;
用线性变换理论推导洛仓兹变换
6) linear transform
线性变换
1.
Some properties of general linear transform;
广义线性变换的若干性质
2.
This paper discusses a method that facilitates the application of 3-D AVO methods in reservoir prediction through Zoeppritz equation linear transform.
通过对Zoeppritz方程作线性变换,可以使三维AVO方法便捷地应用于储层预测。
3.
The concept is introduced of the annihilating polynomial and minimal polynomial of vector with linear transform, their property discussed.
介绍了线性变换作用向量的化零多项式与最小多项式的概念,并讨论了它们的性质。
补充资料：线性变换
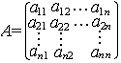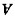| 线性变换 linear transformation 线性代数研究的一个对象，向量空间到自身的保运算的映射。例如，对任意线性空间V，位似σk：a  ka是V的线性变换，平移则不是V的线性变换，若a1，…，an是V的基，σ（aj）＝a1ja1＋…＋anj（j＝1，2，…，n），则称 为σ关于基｛a：｝的矩阵。对线性变换的讨论可藉助矩阵实现。σ关于不同基的矩阵是相似的。Kerσ＝｛a∈V｜σ（a）＝θ｝（式中θ指零向量）称为σ的核，Imσ＝｛σ（a）｜ a∈V｝称为σ的象，是刻画σ的两个重要概念。对于欧几里得空间，若σ关于标准正交基的矩阵是正交（对称）矩阵，则称σ为正交（对称）变换。正交变换具有保内积、保长、保角等性质，对称变换具有性质：〈σ(a)，β〉＝〈a，σ（β）〉。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条