1) f-matrixes of linear transform


线性变换的f-矩阵
3) elementary transformations of a matrix on the Matrix Ring F[A]


F[A]上矩阵的初等变换
4) linearity transformation matrix


线性变换矩阵
5) invariability of matrix transformation


变换矩阵的不变性
6) linearization matrix of the renormalization group


重正化群的线性化变换矩阵
补充资料:线性变换
| 线性变换 linear transformation 线性代数研究的一个对象,向量空间到自身的保运算的映射。例如,对任意线性空间V,位似σk:a 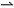 ka是V的线性变换,平移则不是V的线性变换,若a1,…,an是V的基,σ(aj)=a1ja1+…+anj(j=1,2,…,n),则称 ka是V的线性变换,平移则不是V的线性变换,若a1,…,an是V的基,σ(aj)=a1ja1+…+anj(j=1,2,…,n),则称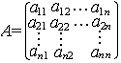 为σ关于基{a:}的矩阵。对线性变换的讨论可藉助矩阵实现。σ关于不同基的矩阵是相似的。Kerσ={a∈V|σ(a)=θ}(式中θ指零向量)称为σ的核,Imσ={σ(a)| 为σ关于基{a:}的矩阵。对线性变换的讨论可藉助矩阵实现。σ关于不同基的矩阵是相似的。Kerσ={a∈V|σ(a)=θ}(式中θ指零向量)称为σ的核,Imσ={σ(a)|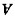 a∈V}称为σ的象,是刻画σ的两个重要概念。 a∈V}称为σ的象,是刻画σ的两个重要概念。对于欧几里得空间,若σ关于标准正交基的矩阵是正交(对称)矩阵,则称σ为正交(对称)变换。正交变换具有保内积、保长、保角等性质,对称变换具有性质:〈σ(a),β〉=〈a,σ(β)〉。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条