1) pseudo-integral equation


伪积分方程
2) Linear Quasi-parabolic Integro-differential Equation


伪抛物型积分微分方程
1.
(1) Linear Quasi-parabolic Integro-differential Equation(2)Linear Quasi-hyperbolic Integro-differential EquationWe obtain Lp-optimal and W1,p- optimal estimats under the certain condition(2 ≤ p < ∞).
本文的第一、二章分别考虑(1)伪抛物型积分微分方程的初边值问题(2)伪双曲型积分微分方程的初边值问题的有限元超收敛结果。
3) Linear Quasi-hyperbolic Integro-differential Equation


伪双曲型积分微分方程
1.
(1) Linear Quasi-parabolic Integro-differential Equation(2)Linear Quasi-hyperbolic Integro-differential EquationWe obtain Lp-optimal and W1,p- optimal estimats under the certain condition(2 ≤ p < ∞).
本文的第一、二章分别考虑(1)伪抛物型积分微分方程的初边值问题(2)伪双曲型积分微分方程的初边值问题的有限元超收敛结果。
5) integral equation


积分方程
1.
Computation of array induction logging response using integral equations;


利用积分方程计算阵列感应测井响应
2.
Multi-constraint smooth method for solving fredholm integral equation of first kind;


第一类Fredholm积分方程的多重约束光滑化方法
3.
Elimination of the singularity of integrands in the integral equation of harmonic electromagnetic field;
交变电磁场积分方程被积函数奇异性的消除
6) Integral equations


积分方程
1.
Study of live line measurement of parameters of transmission lines with mutual inductance based on integral equations;
基于积分方程的互感线路参数带电测量研究
2.
The application of fixed point theoretics to a kind of integral equations;


不动点理论在解一类积分方程中的应用
3.
But the abailable first or the second kind of integral equations are illposed, so that the regularization methods are used.
积分方程方法是求解波动逆问题的一种新的方法 ,它利用积分算子有效地将散射物边界数据遇射到远场或者近场测试的数据上 ,在已知散射物的初始物形和一些特征时 ,能给出较好的重构效果 ;但是 ,所得的第一类和第二类积分方程是不适定的 ,这样就需要用到正则化方法。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 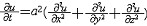 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式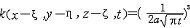 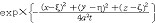 热传导方程初值问题的解可用基本解叠加而成,即 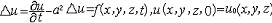 的解为 的解为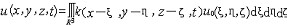 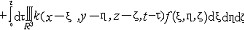 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 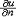 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条