1) orientation of manifold
流形的定向
2) non-orientable manifold
不可定向的流形
3) oriented manifold
定向流形
4) orientable manifold
可定向流形
5) oriented compact manifold
定向紧流形
6) oriented pseudo-manifold
定向伪流形
补充资料：流形
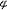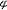| 流形 manifold 一类特殊的连通、豪斯多夫仿紧的拓扑空间。在此空间每一点的邻近预先建立了坐标系，使得任何两个（局部）坐标系间的坐标变换都是连续的。这里所说在一点邻近建立坐标系就是：存在这个点的一个邻域U和一个同胚映射  ：U→V，其中V是某个欧氏空间Rn中的开集。这样的 可看成U上n个函数，它们就给出U中点的坐标。在上面流形的定义中，若坐标变换皆是连续可微的，则进一步称空间为微分流形。流形的概念最早是由B.黎曼在1854年提出的。流形最重要的特性是：有局部坐标系。这个特性并不奇特，以至流形能广泛地出现在物理、几何问题之中。同时这个特性又使人们可系统地运用坐标方法，从而导致富有成效的研究。因此流形成为数学中一个重要概念。 对流形的研究还有一套组合方法，H.庞加莱对这种方法的出现起了决定性作用。那是预先假定流形“剖分”成一些单形之和，使各单形之间是规则相处的。从“剖分”出发，创造出链群和边缘算子概念，再用有限的代数算法导出同调群，进而开展研究（见同调论）。 关于流形的重要结果有：斯托克斯公式，示性类，德·拉姆同构，对偶定理。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条