1) Set Theory & Algebraical Structure


集合论与代数结构
2) structural theory of algebra


代数结构论
3) the functions relating to algebraic structure


代数结构函数论
1.
At the end of this paper, the problem of researching the functions relating to algebraic structure is brought forward.
在讨论代数结构抽象性的基础上引入了反映代数结构的类数(随基数)变化情况的伴随函数的概念;然后主要利用对合自同构和直积,从给定结构之内、外两个方面的变换出发,给出了构造具有相同伴随函数的代数结构的两种方法;并指出,伴随函数的概念有助于拓广人们对代数结构的认识;文末一般地提出了代数结构函数论的研究问题。
4) algebraic structure theory


代数结构理论
5) associative isomorphism


结合代数同构
6) algebraic structure


代数结构
1.
The effect of algebraic structure breaking of Hamiltonian on geometric phase;


代数结构破缺对几何相位的影响
2.
On the algebraic structure of Klimov-Shamir T-function;


Klimov-Shamir T-函数的代数结构
3.
This paper proposes a integration model of OLAP and mining association rules by analyzing the characteristics of mining association rules and OLAP, and gives its algebraic structure description.
通过分析关联规则挖掘和联机分析处理 (OL AP)的特点 ,提出了一种联机分析处理与关联规则挖掘的集成化模型 ,并给出了其代数结构描述 ;在此基础上 ,提出了一种基于 OL AP的关联规则挖掘理论 ,从而为简化挖掘步骤 ,提高挖掘效率奠定了理论基础 ;使用超市的实际数据进行实验分析 ,验证了该模型及其挖掘理论的正确性和可行性 。
补充资料:集合论
| 集合论 set theory 以一般集合为研究对象的一个数学分支。由于数学的大多数分支所研究的对象或者可以看成某种特定结构的集合 ,或者可以通过集合来定义,因此集合论的基本概念已渗透到数学的几乎一切领域,从而可以说集合论已是整个现代数学的基础。 集合论是在19世纪末由德国数学家G.康托尔创立的 。它的发展可分为两个阶段:1908 年以前称为朴素集合论 ;1908年以后称为公理集合论。康托尔于1874年超越数集的局限 ,首先建立起一般性的集合概念 。康托尔的重大成就在于对无穷集的研究,为了刻画无穷集所含元素的数量,康托尔引进集合的基数(势)的概念,元素间能建立一一对应的集合称为等基数(等势)集,于是基数便是可以建立一一对应的集合类的抽象,反映这类集合的共同的数量特征。有限集的基数就是通常意义下的“个数”即自然数,无限集的基数是“个数”概念的推广,康托尔证明了有理数集是可数集(即能与自然数集建立一一对应)之后,又意外地发现实数集是不可数集,并给出了证明,这个事实说明实数集和有理数集的基数是不同的,从而揭示了无穷集之间在元数数量上存在着层次的差别,把有限集大小的概念推广到无穷集 ,还可以比较任意两个基数的大小,康托尔证明了任一集合A的基数 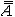 小于它的幂集P(A)的基数 小于它的幂集P(A)的基数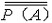 ,即 ,即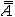 < <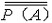 ,对于自然数集N,就有 ,对于自然数集N,就有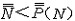 。再做P(N)的幂集,就有 。再做P(N)的幂集,就有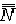 < <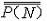 < < ,不断做下去,就得到一个基数序列 ,这就是说在所有无穷集之间还存在着无穷多个层次。除此以外,为了描绘任一良序集的结构,康托尔还建立了序数概念,将用来编序的自然数(第一、第二、第三、…)加以推广 ,利用序数可以把良序集编号,进而把数学归纳法推广到自然数以外去。康托尔对无穷集的研究成果对数学的发展产生了深远的影响。 ,不断做下去,就得到一个基数序列 ,这就是说在所有无穷集之间还存在着无穷多个层次。除此以外,为了描绘任一良序集的结构,康托尔还建立了序数概念,将用来编序的自然数(第一、第二、第三、…)加以推广 ,利用序数可以把良序集编号,进而把数学归纳法推广到自然数以外去。康托尔对无穷集的研究成果对数学的发展产生了深远的影响。在1900年前后,由于集合论本身的不够协调而相继地产生了一些悖论 ,使集合论受到非难 。按照集合论的观点,一切集合构成一个集合V,集合V 的基数不应小于任何其他集合的基数,但是根据康托尔定理,却必须小于幂集 P(V)的基数,这就自相矛盾(康托尔悖论,1899年)。又如,把所有不属于自身(即不包含自身作为元素)的集合组成一个集合R,问R是否属于R?如果说R属于R,那么R满足R 的定义,R不属于自身,即R不属于R;如果说R不属于R,那么R 不满足定义,即R应属于自身,那么R属于R。无论怎么说,都自相矛盾(罗素悖论,1903年)。在各种悖论中的罗素悖论最为简明,只涉及属于、不属于两个概念,引起了数学界的震惊。悖论的出现使人们对集合论产生了怀疑,甚至对整个数学推理的正确性也产生了疑问,这就动摇了数学的基础,触发了数学史上的第三次危机。经过数学家们潜心研究,认识到悖论产生的原因在于康托尔原来的集合定义是不严格的 ,按照原来的定义,不能否认“所有集合组成的集合”也是一个集合,也不能排除满足条件“不包含自己作为元素的集合”的事物构成一个集合,可见,为了避免悖论,必须对集合的定义加以严格的限制。 康托尔集合论中的集合,作为一个原始概念,很难对它的定义给出适当的限制使得避免悖论而又保留集合论中一切有价值的东西。数学家们经过一番努力之后,终于放弃直接提出集合的定义 ,而选择了公理化方法 ,重新整理集合论。1908 年E.F.F.策梅洛提出了一个公理化的方案,其公理系统以集合和属于为仅有的两个不加定义的原始概念,其余有外延公理、空集存在公理、无序对集合存在公理、并集公理、幂集公理、无穷公理、分离公理、选择公理等。后来经过A.A.弗伦克尔和 A.T.斯科朗的改进,又补充了替换公理和正则公理,通称ZF公理系统,ZF公理系统集合论,对于排除康托尔朴素集合论的悖论和继承原有成果是相当成功的。除ZF公理系统外,还有多种其他系统,如1925~1937年形成的J.冯·诺伊曼、P.贝尔奈斯、K.哥德尔的公理系统,称为NBG 公理系统。无论哪种公理系统,都使朴素集合论得到严格处理,避免悖论,保留一切有价值的东西,使集合论进入一个更新的发展阶段。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条