1) non euclidean space


非欧几里得空间
2) Euclidean space


欧几里得空间
1.
In this paper the authors generalize 1-independentvariable the integral inequalities by Gronwall and establish the integral inequalities in the n-dimensional Euclidean space R~n.
将一维函数的Gronwall不等式推广到了n维欧几里得空间。
2.
In this paper,the operation of vectors of Euclidean space Rn has been carried on the new definition and two inequalities about the operation of vectors are given.
对欧几里得空间Rn中的向量定义了新的运算,推出了两个关于向量运算的不等式。
3) pseudo-Euclidean space


伪欧几里得空间
4) euclidean vector space


欧几里得向量空间
5) locally euclidean space


局部欧几里得空间
补充资料:欧几里得空间
| 欧几里得空间 Euclidean space 一类特殊的向量空间。对通常3维空间V3中的向量可以讨论长度、夹角等几何性质。若a=(a1,a2,a3),β=(b1,b2,b3),则a的长度  a与β的内积 a与β的内积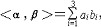 a与β的夹角a,β=arccos a与β的夹角a,β=arccos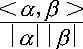 (假定a,β均非零向量)。推广之,在n维向量空间Rn中,若a=(a1,……,an),β=(b1,……,bn),规定 (假定a,β均非零向量)。推广之,在n维向量空间Rn中,若a=(a1,……,an),β=(b1,……,bn),规定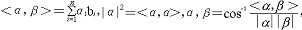 它具有类似的几何性质。Rn连同运算<,>,称为一个欧几里得空间。更一般地,若V是R上向量空间,称V×V到R的一个满足一定条件的映射为内积,带有内积的空间称为欧几里得空间。若<a,β>=0,称a与β正交(垂直)。若V的一个基中的向量两两正交且长度为1,则称为标准正交基,V3中常用的直角坐标系就是标准正交基。每个n维欧几里得空间存在标准正交基,可由任意基改造而得。 它具有类似的几何性质。Rn连同运算<,>,称为一个欧几里得空间。更一般地,若V是R上向量空间,称V×V到R的一个满足一定条件的映射为内积,带有内积的空间称为欧几里得空间。若<a,β>=0,称a与β正交(垂直)。若V的一个基中的向量两两正交且长度为1,则称为标准正交基,V3中常用的直角坐标系就是标准正交基。每个n维欧几里得空间存在标准正交基,可由任意基改造而得。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条