1) congruent number


同余数
1.
A sufficient and necessary condition of the congruent number has been given by fundamental methods of number theory and n is proved to be the sufficient and necessary condition for integer congruent number.
通过运用初等数论的方法,给出同余数的一个充要条件,证明n是整同余数的充要条件,应用实例说明同余数的求解。
2.
The original congruent number formula has been deduced by fundmental methods of number theory.
通过运用初等数论方法,推导出本原同余数公式。
2) algebraic congrue nce algorithms


代数同余
3) integer congruent number


整同余数
1.
A sufficient and necessary condition of the congruent number has been given by fundamental methods of number theory and n is proved to be the sufficient and necessary condition for integer congruent number.
通过运用初等数论的方法,给出同余数的一个充要条件,证明n是整同余数的充要条件,应用实例说明同余数的求解。
4) congruent array


同余数组
5) congruence zeta function


同余函数
6) congruent integers


同余整数
补充资料:同余
| 同余 congruence 给定一个正整数m,把它叫做模。如果用m去除任意两个整数a与b所得的余数相同,就说a、b对模m同余,记作a≡b(mod m)。如果余数不同,就说a、b对模m不同余,记作a 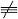 b(mod m)。 b(mod m)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条