1) jet geometry


射流几何学
2) projection geometry


射影几何学
1.
Abstract: Some basic ways of proving three lines share one point from the view points of analyticgeometry and projection geometry are expounded in this essay.
从仿射几何学与射影几何学的基本方法出发,简述了“三线共点”问题的一些基本的证明方法。
3) affine geometry


仿射几何[学]
4) Flow geometry


流动几何学
5) geometry of mainfold


流形几何学
6) channel geometry


流道几何学
补充资料:射影几何学
| 射影几何学 projective geometry 研究图形在射影变换下不变性的一个几何学分支。射影几何学产生的最初动力,来自为了帮助绘画而对透视进行的研究。在17世纪,G.德扎格和B.帕斯卡建立了射影几何学中著名的定理。后来在19世纪,又经过J.V.彭赛列、J.施泰纳、K.G.C.von施陶特、A.F.麦比乌斯、A.凯莱等几何学家的工作,使射影几何学得到蓬勃的发展,达到鼎盛的时期。 经过有限次两平面间的中心投影(透视)得到的平面上的一一点变换,称为平面上的射影变换。对于直线上的4点A,B,C,D,把各有向线段的量之间的比值 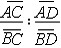
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |