1) generalized Euclidean Steiner problem


广义欧几里德Steiner问题
2) Euclidean 2-connected Steiner network problem


欧几里德2-连通Steiner网络问题
1.
The Euclidean 2-connected Steiner network problem is to determine the minimum-weight 2-connected Steiner network on a given set of points in the Euclidean plane.
所谓欧几里德2-连通Steiner网络问题,就是对于给定的平面点集P,确定它的长度最小的2-连通Steiner网络,该问题与组合最优化中著名的Steiner问题和旅行售货员问题有关,同时在水、电供应网络和通讯网络等设计中也有非常广泛的应用,所以对该问题的研究具有重要的意义。
2.
Given a finite set P of points in the Euclidean plane, the Euclidean 2-connected Steiner network problem is to find the shortest 2-connected Steiner network on P, where th.
欧几里德2-连通Steiner网络问题可以描述为:给定欧几里德平面上的一个有限点集P,确定P的最短2-连通Steiner网络。
3) generalized Steiner problem


广义Steiner问题
4) the shortest 2-connected Steiner network


最短欧几里德2-连通Steiner网络
5) Europead


欧几里德
1.
Examination of the possible world in Europead s geometrical system based on pure deduction;
对欧几里德几何体系之可能世界的考察——以纯粹演绎的观点为基础
6) Euclidear alsorithm


欧几里德法
补充资料:非欧几里得几何学
| 非欧几里得几何学 geometry,nonEuclidean 一般指罗巴切夫斯基几何(又称双曲几何和黎曼椭圆几何)。简称非欧几何。它们与欧几里得几何最主要的区别在于公理体系中采用了不同的平行公理。
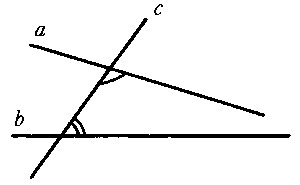
诞生 欧几里得几何学中的平行公理(通过直线外一点至多有一条直线与已知直线共面不交)与《几何原本》一书中的第五公设〔如果两条直线与另一条直线相交,所成的同侧内角之和小于两直角 ,那么这两条直线在这一侧必相交(图1)〕相等价,《几何原本》中前4个公设叙述简单,几何含意明显,而第五公设则不同,很像一条定理。于是许多数学家都尝试根据其他公理、公设来证明它,这就是历史上著名的第五公设问题。第五公设的证明持续了2000年之久,结果均告失败。失败的原因不外是暗用了第五公设的等价命题或在证明过程中用了未经证明的判断。然而正是这些“失败”的工作,给非欧几何的创立准备了必要的条件。到了19世纪,俄国数学家N.I.罗巴切夫斯基企图用归谬法证明第五公设,他把欧几里得第五公设以外的公设、公理都保留,只把第五公设改换成与它相反的命题作为一个公理,如此推证下去如果出现矛盾,则假设是错误的,于是第五公设必然成立。可是他推证了一连串的命题都没有发现矛盾,而出现了一个新的几何体系。罗巴切夫斯基认为这个新体系代表一种新的几何学,他称之为虚几何学。这种几何不同于欧几里得几何,所以称之为非欧几里得几何学,罗巴切夫斯基于1826年2月23日在喀山大学数学会上宣读了题为《几何学原理的扼要阐释及平行线定理的严密证明》的论文,这一天就是非欧几何诞生的日子。当时德国数学家C.F.高斯和匈牙利的J.波尔约也独立地发现了非欧几何。非欧几何的创建,导致了人们对几何基础的深入研究。
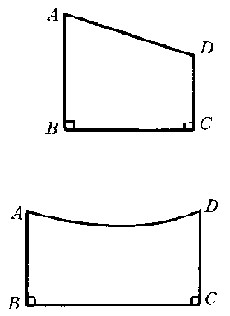
罗巴切夫斯基几何与欧几里得几何 19世纪末期,德国数学家D.希尔伯特建立了一个完善的欧几里得几何学的公理系统,从而使得《几何原本》中的欠缺都得以弥补。由希尔伯特公理体系中的结合、顺序、合同、连续4组公理所建立的几何体系称为绝对几何,再加上欧几里得平行公理就是欧几里得几何;如果绝对几何公理体系加上一条罗巴切夫斯基平行公理(通过直线外一点至少有两条直线与已知直线共面不相交)就成为罗巴切夫斯基几何。由于发现了罗巴切夫斯基几何,才结束了求证第五公设的工作。绝对几何是欧几里得几何与罗巴切夫斯基几何的公共部分,就是说绝对几何的定理在欧几里得、罗巴切夫斯基两种几何中都成立,例如:任何三角形内角和不大于π,设四边形ABCD中,∠ABC,∠BCD是直角(图2),且AB≥CD,则∠A≤∠D,等均是绝对几何中的定理,上述后一命题中的双直角四边形,若有AB与DC相等,则称之为萨开里四边形或等腰双直角四边形,∠A、∠D称为其顶角,AD、BC分别为其上底和下底。命题“萨开里四边形顶角不大于直角,且其上、下底中点连线垂直于上、下底”,也是绝对几何定理,这些都是欧、罗两种几何的共同点。不同点在于平行公理,而罗巴切夫斯基平行公理正是欧几里得平行公理的相反命题(否定命题),由是得出罗巴切夫斯基几何中许多与欧几里得几何相违背的定理,例如:①共面不交二直线被第三线所截同位角(或内错角)不一定相等。②在平面上,一直线的垂线、斜线不一定相交。③三角形内角和小于两个直角。④两个三角形若有三对角对应相等,则此两三角形全等(即不存在相似而不全等的三角形)。⑤萨开里四边形顶角小于直角(这说明在罗巴切夫斯基平面上不存在矩形)。⑥通过不共线三点不一定能作一个圆。⑦三角形三边高线不一定交于一个点。⑧通过直线外一点与已知直线共面不相交的直线有无数条 。因为通过一条直线a外一点A,有无数条直线与a相交,由命题⑧知,又有无数条直线与a不相交,与直线a相交与不相交的界线(它本身是不相交的直线),共有两条,称为直线a的沿方向 AA′和AA″的平行线,故在罗氏平面上,通过直线外一点有两条直线于不同方向平行于已知直线。 黎曼椭圆几何与欧几里得几何 另一种非欧几何黎曼椭圆几何是德国数学家B.黎曼于1854年提出的,这种几何的公理体系较之欧几里得几何有较大的差别,它用“在平面上,任何两条直线一定相交”代替欧几里得平行公理。在这种几何里“任何三角形三内角和大于两直角”。如果把球面上的一对对经点看作为一个点,就可以得到这种非欧几何。非欧几何与欧几里得几何表面上矛盾,但各自都反映了现实空间的相对真理。 影响 非欧几何的建立不仅拓广了几何学观念,而且在数学一些分支中有着重要应用,同时对于物理学在20世纪初期关于时空观念的变革也起了重大作用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条