1) Jacobi ellipse function method


Jacobi从椭圆函数展开法
2) Jacobi elliptic function expansion method


Jacobi椭圆函数展开法
1.
Extended Jacobi elliptic function expansion method and its application;


扩展Jacobi椭圆函数展开法及其应用
2.
By the truncated expansion and Jacobi elliptic function expansion methods, we have found some exact solitary wave, rational formal, triangle function and elliptic periodic solutions of the general variable coefficient KdV equation with external force term.
运用截断展开法和Jacobi椭圆函数展开法,求得了含外力项的广义变系数KdV方程的精确孤立波解、有理形式函数解、三角函数解和椭圆周期解。
3.
We will attempt to solve a coupled KdV equations by using two methods which are very effective in solving a large class of nonlinear evolution equations,namely,Jacobi elliptic function expansion method and F-expansion method.
尝试用Jacobi椭圆函数展开法和F展开法来求解耦合KdV方程组。
3) Jacobi elliptic function rational expansion method


Jacobi椭圆函数有理展开法
1.
The extend Jacobi elliptic function rational expansion method was applied to the Boussinesq equation.
应用扩展的Jacobi椭圆函数有理展开法并辅助符号计算,建立了Boussinesq方程新的Jacobi椭圆双周期波解和相应的三角函数单周期解。
4) Jacobian elliptic function expansion method


Jacobi椭圆函数展开法
1.
Double Jacobian elliptic function expansion method under a general function transform and its applications;
一般变换下双Jacobi椭圆函数展开法及应用
5) Jacobi elliptic function expansion method


Jacobi椭圆函数展开方法
1.
Using the modified Jacobi elliptic function expansion method,the periodic wave solutions for the coupled nonlinear Klein-Gordon equations are obtained.
利用修正的Jacobi椭圆函数展开方法,获得了一类耦合非线性Klein-Gordon方程组的周期解。
6) Jacobi elliptic function expansion


Jacobi椭圆函数展开
1.
On the basis of the principle of homogeneous balance,these equations were resolved by Jacobi elliptic function expansion method and the exact periodic solutions were obtained.
根据齐次平衡原理,用Jacobi椭圆函数展开对这些常微分方程求解,给出了精确的周期解及其模数m→1退化情况下的孤立波解或冲击波解,与定性分析完全一致。
补充资料:椭圆函数
| 椭圆函数 elliptic function 在有限复平面上亚纯的双周期函数。所谓双周期函数是指具有两个基本周期的单复变函数,即存在ω1,ω2两个非0复数, 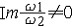 ,而对任意整数n,m,有f(z+nω1+mω2)=f(z) ,于是{nω1+mω2|n,m为整数}构成f(z)的全部周期,在复平面上任取一点a,以a,a+ω1,a+ω1+ω2,a+ω2为顶点的平行四边行的内部 ,再加上两个相邻的边及其交点,这样构成的一个半开的区域称为f(z)的一个基本周期平行四边形,将它平行移动nω1+mω2,当n,m取遍所有整数时,即得一覆盖整个复平面的周期平行四边形网,f(z)在每一个周期平行四边形中的性质都和它在基本周期平行四边形中的一样。在基本周期平行四边形中,f(z)有以下性质:非常数椭圆函数一定有极点,且极点留数之和必为零,因而不可能只有一个一阶极点,有n个极点的椭圆函数称为n阶椭圆函数 ,它在基本周期平行四边形内取任一值n次,即对任意复数A,f(z)-A在基本周期平行四边形内有且仅有n个零点 ,且f(z)的零点之和与极点之和的差必等于一个周期。 ,而对任意整数n,m,有f(z+nω1+mω2)=f(z) ,于是{nω1+mω2|n,m为整数}构成f(z)的全部周期,在复平面上任取一点a,以a,a+ω1,a+ω1+ω2,a+ω2为顶点的平行四边行的内部 ,再加上两个相邻的边及其交点,这样构成的一个半开的区域称为f(z)的一个基本周期平行四边形,将它平行移动nω1+mω2,当n,m取遍所有整数时,即得一覆盖整个复平面的周期平行四边形网,f(z)在每一个周期平行四边形中的性质都和它在基本周期平行四边形中的一样。在基本周期平行四边形中,f(z)有以下性质:非常数椭圆函数一定有极点,且极点留数之和必为零,因而不可能只有一个一阶极点,有n个极点的椭圆函数称为n阶椭圆函数 ,它在基本周期平行四边形内取任一值n次,即对任意复数A,f(z)-A在基本周期平行四边形内有且仅有n个零点 ,且f(z)的零点之和与极点之和的差必等于一个周期。在以上性质的规范下 ,有两大类重要的椭圆函数:①魏尔斯特拉斯-δ函数。它表作 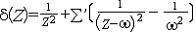 ,其中ω=2nω1+2mω2,Σ'表n,m取遍全部整数之和 ,但要除去ω=0的情形。这是一个二阶椭圆函数,在周期平行四边形中,仅有一个ω是二阶极点,ω=δ(z)满足微分方程(ω′)2=4ω3-g2ω-g3,其中g2=60Σ' ,其中ω=2nω1+2mω2,Σ'表n,m取遍全部整数之和 ,但要除去ω=0的情形。这是一个二阶椭圆函数,在周期平行四边形中,仅有一个ω是二阶极点,ω=δ(z)满足微分方程(ω′)2=4ω3-g2ω-g3,其中g2=60Σ'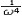 g3=140Σ' g3=140Σ'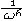 ,由此可见ω=δ(z)是 ,由此可见ω=δ(z)是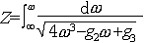 的反函数,右边的积分称为椭圆积分。可以证明,所有的椭圆函数都可以用δ(z)函数来表示 ,而每一个椭圆函数都一定满足一个常系数一阶的代数微分方程。②雅可比椭圆函数。它定义为椭圆积分 的反函数,右边的积分称为椭圆积分。可以证明,所有的椭圆函数都可以用δ(z)函数来表示 ,而每一个椭圆函数都一定满足一个常系数一阶的代数微分方程。②雅可比椭圆函数。它定义为椭圆积分 的反函数 ,记作ω=J(z),J(z)的基本周期平行四边形是一个矩形 ,其基本周期是4K与2iK′,此处 的反函数 ,记作ω=J(z),J(z)的基本周期平行四边形是一个矩形 ,其基本周期是4K与2iK′,此处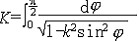 , ,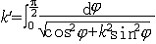 ,其二阶极点为iK′,而k是一个实常数。 ,其二阶极点为iK′,而k是一个实常数。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条