1) subharmonic-harmonic
子谐波-谐波
2) subharmonic-harmonic
子谐波谐波
1.
Energy-spectrum entropy and subharmonic-harmonic rate methods were used to analyze speech based on speech sinusoidal model.
基于语音正弦模型,采用能量谱熵和子谐波谐波比率方法进行语音分析。
3) sub-harmonic
子谐波
1.
An improving sub-harmonic to harmonic ratio(ISHR)algorithm based on sub-harmonic to harmonic ratio(SHR)and using the voiced speech harmonic and sub-harmonic in the speech sinusoidal model algorithm was proposed.
利用正弦语音模型中浊音存在的谐波与子谐波,在SHR(subharninctoharmonicratio)算法的基础上,提出了一种改进型高精度基音检测算法ISHR(improvingsubharninctoharmonicratio)。
4) quantum harmonic oscillator
量子谐振子
1.
Comparison of quantum harmonic oscillator and classical harmonic oscillator;
量子谐振子与经典谐振子的比较
2.
In this paper,the author deduces the momentum-position uncertainty relation of the classical harmonic oscillator,and gives the correspondence relation between it and the uncertainty relation of quantum harmonic oscillator.
推出了经典谐振子的动量-位置不确定关系,并且给出它和量子谐振子的不确定关系之间的对应关系。
3.
The evolution problem of two quantum harmonic oscillators with ccordinate and mo-mentum first-order coupling is studied. The exact solution is derived by introducing appropriate oper-aters and auxiliary functionals.
提出了具有坐标和动量一阶耦合的两量子谐振子的演化问题。
5) quantum oscillator
量子谐振子
1.
By using the general linear quantum transformation theory, the quantum oscillator is solved, and the condition of the quantum oscillator tend to classical limit is given by analogy with classicaloscillator.
运用广义线性量子变换的普遍理论求解了量子谐振子 ,同经典谐振子类比给出了量子谐振子趋近于经典极限的条件 ,相干态是最理想的经典极限态 。
2.
By analysing one-dimensional quantum oscillator,the classical limit conditions of the quantum system also expresses as →0.
以一维量子谐振子为例,经过分析,认为量子系统经典极限条件也可表示为 h→0。
6) two-photon resonance
双光子谐振
1.
In this paper,cyclic commutation relations of the set of spin-one operators Jx, {Jx,Jy}and {Jz,Jx} are used to simplify and obtain a formal solution to the time evolution of a three-level atom in two-photon resonance with two laser fields which are fully amplitude modulated in quadrature.
本文利用自旋为1的算符Jx,{Jx,Jy}和{Jz,Jx}的循环交换关系,在位相差为的两模激光场振幅调制中考虑双光子谐振,得到了三能级原子的时间演化规律,并讨论粒子数俘获。
参考词条
量子谐振系统
电子谐振电路
[电子]谐波干扰场
表面等离子谐振效应
耗散介观电子谐振腔
二维耦合量子谐振子
氢氧根离子谐波吸收<光>
三模坐标-动量耦合量子谐振子
多维耦合受迫量子谐振子
聚合酶链式反应-序列特异性引物(PCR-SSP)
键式离合器
补充资料:传动:谐波传动
由波发生器﹑柔性件和刚性件 3个基本构件组成的机械传动。这种传动是在波发生器的作用下﹐使柔性件產生弹性变形并与刚性件相互作用而达到传递运动或动力的目的。在传动中波发生器迴转一周﹐柔性件上某一点循环变形的次数称波数。柔性件的变形过程是一个基本对称的谐波(图1 双波柔轮的变化波形 )﹐故称为谐波传动。常用的谐波传动是双波传动。
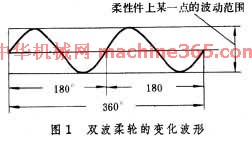
图2 谐波齿轮结构示意图 为一个外周有许多齿( 120个以上)的柔轮与一个内周有齿的刚轮相嚙合进行传动﹐称为谐波齿轮传动。假设将齿数无限增多﹐齿高也无限减小﹐则成为柔轮外表面和刚轮内表面在波发生器长轴方向上进行接触的谐波摩擦传动。由於这种接触点的摩擦力很小﹐传递的力矩不大﹐容易打滑﹐实际上应用很少。谐波传动也可以设计成由转动改为直线运动﹐成为谐波螺旋传动。在3种传动中以谐波齿轮传动应用最广。图2 谐波齿轮结构示意图 中波发生器是机械式波发生器﹐此外还有电磁式﹑液力式和气动式的波发生器﹐其中机械式波发生器应用最普遍。

谐波传动是美国人C.W.马瑟於1955年提出的专利﹐1959年得到批准﹐1960年在纽约展出实物。谐波传动的发展是由军事和尖端技术开始的﹐以后逐渐扩展到民用和一般机械上。一些国家如美国﹑日本﹑苏联已有了谐波齿轮减速器的系列化產品﹐在中国也制定了谐波齿轮的部颁标準。
工作原理 以谐波齿轮传动为例。它是利用柔轮﹑刚轮和波发生器的相对运动﹐特别是柔轮的可控弹性变形(形状改变)来实现运动和动力传递的。在这 3个基本构件中可任意固定一个﹐其餘一个为主动件一个为从动件。如果3个都不固定﹐则成为差动轮系。如以刚轮固定不变﹐以波发生器为主动件﹐柔轮为从动件﹐波发生器内的椭圆形凸轮在柔轮内旋转便使柔轮產生变形。在波发生器的椭圆形凸轮长轴两端处的柔轮轮齿和刚轮轮齿进入嚙合时﹐短轴两端处的柔轮轮齿与刚轮轮齿脱开。对於波发生器长轴和短轴之间的齿﹐沿柔轮和刚轮周长的不同区段内处於逐渐进入嚙合的半嚙合状态﹐称为嚙入﹔处於逐渐退出嚙合的半嚙合状态﹐称为嚙出。波发生器的连续转动﹐使嚙入﹑嚙合﹑嚙出和脱开四种运动不断改变各自原来的工作状态﹐这种运动称为错齿运动。错齿运动使输入转动变为输出运动。若刚轮固定不动﹐柔轮则相对於波发生器作反方向的转动。反之若柔轮固定不动﹐刚轮则相对於波发生器作同方向的转动。对於双波传动的谐波齿轮传动﹐它的转动规律是﹕波发生器转一周﹐柔轮相对於刚轮在周长方向转过两个齿距的弧长﹐其转动比计算如下﹕

图2 谐波齿轮结构示意图 为一个外周有许多齿( 120个以上)的柔轮与一个内周有齿的刚轮相嚙合进行传动﹐称为谐波齿轮传动。假设将齿数无限增多﹐齿高也无限减小﹐则成为柔轮外表面和刚轮内表面在波发生器长轴方向上进行接触的谐波摩擦传动。由於这种接触点的摩擦力很小﹐传递的力矩不大﹐容易打滑﹐实际上应用很少。谐波传动也可以设计成由转动改为直线运动﹐成为谐波螺旋传动。在3种传动中以谐波齿轮传动应用最广。图2 谐波齿轮结构示意图 中波发生器是机械式波发生器﹐此外还有电磁式﹑液力式和气动式的波发生器﹐其中机械式波发生器应用最普遍。

谐波传动是美国人C.W.马瑟於1955年提出的专利﹐1959年得到批准﹐1960年在纽约展出实物。谐波传动的发展是由军事和尖端技术开始的﹐以后逐渐扩展到民用和一般机械上。一些国家如美国﹑日本﹑苏联已有了谐波齿轮减速器的系列化產品﹐在中国也制定了谐波齿轮的部颁标準。
工作原理 以谐波齿轮传动为例。它是利用柔轮﹑刚轮和波发生器的相对运动﹐特别是柔轮的可控弹性变形(形状改变)来实现运动和动力传递的。在这 3个基本构件中可任意固定一个﹐其餘一个为主动件一个为从动件。如果3个都不固定﹐则成为差动轮系。如以刚轮固定不变﹐以波发生器为主动件﹐柔轮为从动件﹐波发生器内的椭圆形凸轮在柔轮内旋转便使柔轮產生变形。在波发生器的椭圆形凸轮长轴两端处的柔轮轮齿和刚轮轮齿进入嚙合时﹐短轴两端处的柔轮轮齿与刚轮轮齿脱开。对於波发生器长轴和短轴之间的齿﹐沿柔轮和刚轮周长的不同区段内处於逐渐进入嚙合的半嚙合状态﹐称为嚙入﹔处於逐渐退出嚙合的半嚙合状态﹐称为嚙出。波发生器的连续转动﹐使嚙入﹑嚙合﹑嚙出和脱开四种运动不断改变各自原来的工作状态﹐这种运动称为错齿运动。错齿运动使输入转动变为输出运动。若刚轮固定不动﹐柔轮则相对於波发生器作反方向的转动。反之若柔轮固定不动﹐刚轮则相对於波发生器作同方向的转动。对於双波传动的谐波齿轮传动﹐它的转动规律是﹕波发生器转一周﹐柔轮相对於刚轮在周长方向转过两个齿距的弧长﹐其转动比计算如下﹕
说明:补充资料仅用于学习参考,请勿用于其它任何用途。