1) Hirota bilinear operator


Hirota双线性算子
1.
Next, in Hirota bilinear operator extended to the supersymmetrical situatio.


其次,在Hirota双线性算子推广到超对称的情形下,给出了许多重要的超对称双线性恒等式,并应用它们求得了B(?)cklund变换和孤波解。
2) Hirota bilinear forms


Hirota双线性型
3) Hirota bilinear form


Hirota双线性形式
1.
Hirota bilinear form of the Caudrey-Dodd-GibbonKaeada(CDGK)equations is got by Painleve Truncated method,and in accordance with its bilinear and by using Hirota bilinear methods,a single solution and double soliton solutions of CDGK equations are calculated,then a detailed analysis is made.
利用Painleve截断展开法得到Caudrey-Dodd-Gibbon-Kaeada(CDGK)方程的Hirota双线性形式,并根据其双线性形式,利用Hirota双线性方法求出了CDGK方程的单孤子解与双孤子解,并对双孤子解做了详细分析。
2.
The works we have done include: First, using Painleve singularity structure analysis method, we have proved that the coupled Schrodinger -KdV equations admit Painleve property; Second, according to the truncated Painleve expansion technique, rational transformation method and "degree" method, we obtained the Hirota bilinear form of the coupled Schrodinger-KdV equations and t.
本篇论文以非线性偏微分方程理论为基础,结合计算机符号计算,完成了以下四个方面的工作:一、通过对耦合Schr(o|¨)dinger-KdV方程组的Painlevé性质的分析,证明该方程组具有Painlevé性质;二、利用Painlevé截断展开式,求得了Caudrey-Dodd-Gibbon-Kaeada方程以及耦合Schr(o|¨)dinger-KdV方程组的Hirota双线性形式,其中CDGK方程用三种方法求得其双线性形式,并得到了一致的结果。
4) Hirota bilinear method


Hirota双线性方法
1.
Using the Hirota bilinear method,N-soliton solution is obtained for a (2+1)-dimensional nonlinear evolution equation,utt-uxx-uyy-3(u2)xx-uxxxx=0.
研究了一个2 +1维变形Boussinesq非线性发展方程:utt-uxx-uyy-3(u2)xx-uxxxx=0,运用Hirota双线性方法得到它的N孤子解。
2.
In this thesis, based on the Hirota bilinear method, we mainly discuss how to solve various forms of exact solutions.
本论文就是基于Hirota双线性方法来求解孤子方程的各种精确解并构造两类可积偶合系统。
3.
For example,Hirota bilinear method and Wronskian technique are two important tools to deal with soliton problems.
Hirota双线性方法和Wronskian技巧是两种比较常见的求解方法。
5) Hirota bilinearization


Hirota双线性变换
6) Hirotas method


Hirota线性型
补充资料:线性算子
| 线性算子 linear operator 具有线性性质的一类映射。算子是函数概念的发展和拓广,设X,Y 为数域K上的线性空间,以D(T)Ì蘕为定义域,取值于Y 的映射统称为算子。进而,若D(T)为线性子集,算子T具有线性性质:"x ,y∈D(T),"a ,β∈K ,有T(ax+βy)=aT(x)+βT(y),则称T为线性算子。熟悉的积分算子Tf(x)= 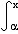 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是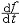 从 从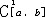 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条