1) linear operator


线性算子
1.
A family of meromorphic multivalent functions defined by a linear operator;


由一个线性算子定义的亚纯多叶函数类
2.
Skew - tripotent preserving linear operators from skew-symmetric matrix spaces to all matrix spaces;
反对称矩阵空间到全矩阵空间的保反立方幂等线性算子
3.
Some properties of a bounded linear operator defined by a g-Bessel sequence;


由g-Bessel序列定义的线性算子的一些性质
2) Linear operators


线性算子
1.
On approximation by linear operators in reiteration interpolation spaces;


用线性算子刻画迭代内插空间
2.
In Part one, the weighted approximation by the linear operators in classical spaces and approximation in Orlicz spaces are studied; In Part two, the approximation of multivariate linear operators is discussed.
本学位论文分为上下两篇,上篇主要为一元线性算子在经典空间的加权逼近和Orlicz空间的逼近:下篇为多元线性算子在经典空间的逼近和加权逼近。
3.
The spectrum of unbounded linear operators was divided into different subsets by the different studying purposes.
无界线性算子谱理论的研究是算子理论的重要研究内容,它能有效地解决现代数学、现代物理学、量子力学中的具体问题。
3) Multilinear operator


多线性算子
1.
In this paper,some multilinear operators related to the Littlewood-Paley operators are defined,and the weighted boundedness for the multilinear operators on some Block-Hardy spaces are obtained by using the atomic and block decomposition of the spaces.
定义一类与L ittlewood-paley算子相关的多线性算子,它是L ittlewood-paley算子的交换子的推广。
2.
The continuity for some multilinear operators related to certain convolution operators on the Triebel-Lizorkin space are obtained.
对一类相关于非卷积型算子的多线性算子,证明了其在Triebel-Lizorkin空间上的连续性,该算子包括Littewood-Paley算子和Marcinkiewicz算子。
3.
In this paper, we prove the endpoint boundedness for some multilinear operators related to certain non-convolution operators.
本文对一类相关于非卷积型算子的多线性算子,证明了其在端点情形上的有界性,该算子包括Littlewood-Paley算子和Marcinkiewicz算子。
4) nonlinear operator


非线性算子
1.
Several stabilities of nonlinear operators;


非线性算子的几种稳定性
2.
The Fréchet derivative of a nonlinear operator and its applications;


一类非线性算子的Fréchet导数及其应用
3.
, Banach space X is uniformly convex and its module of convex (δX(ε)≥)cε~p (0<ε<2,0<c<1,p≥2) if and only if norm of X is satisfied with the inequality ‖(1-(t)x+)ty‖~p+cw(t)‖x-y‖~p≤(1-t)‖x‖~p+t‖y‖~p, x,y∈X, and t∈(0,1), w(t)=(t(1-)t)~p+(1-t)t~p, the authors obtained the convergence of Ishikawa iterative sequences for nonlinear operator.
研究了非线性算子关于由Ishikawa迭代序列的收敛性 ,推广和改进了一些相关的结
5) sublinear operator


次线性算子
1.
Boundedness of sublinear operators on Herz-Morrey spaces;


次线性算子在Herz-Morrey空间上的有界性
2.
The weak estimates for sublinear operators on weighted Herz spaces;


次线性算子在加权Herz空间上的弱型估计
3.
Boundedness of some sublinear operators and commutators on homogeneous Morrey-Herz spaces with non doubling measures
非齐型齐次Morrey-Herz空间中某些次线性算子和交换子的有界性
6) positive linear operators


线性正算子
1.
In this paper,based on classical Korovkin theorem on convergence of positive linear operators,a Korovkin type theorem and more convenient conditions are obtained.
从经典线性正算子收敛的柯洛夫金定理出发,建立了适用范围更广的关于闭区间上连续函数的柯洛夫金定理。
2.
By using of the method of multiplier-enlargement,this paper discusses the asymptotic estimation of approximation of multivariate unbounded continuous functions with positive linear operators,and gives general asymptotic formulae.
利用扩展乘数法讨论了多元线性正算子改造为逼近多元无界连续函数的渐近估计 ,给出了具有一般性的渐近公式 作为实例 ,研究了多元非乘积型的Landau多项式算子逼近多元无界连续函数的渐近估计式 ,推广了前人的若干结
3.
By applying the classical appropriate functions 1, x x2 to the method of multiplier- enlargement, this paper established a certain theorem to approximate any unbounded continuous functions by modified positive linear operators.
将经典“试探函数组”1,x,x2应用于扩展乘数法;建立了一个判别线性正算子能否改造为逼近任意无界连续函数的充要条件。
补充资料:线性算子
| 线性算子 linear operator 具有线性性质的一类映射。算子是函数概念的发展和拓广,设X,Y 为数域K上的线性空间,以D(T)Ì蘕为定义域,取值于Y 的映射统称为算子。进而,若D(T)为线性子集,算子T具有线性性质:"x ,y∈D(T),"a ,β∈K ,有T(ax+βy)=aT(x)+βT(y),则称T为线性算子。熟悉的积分算子Tf(x)= 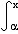 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是 f(t)dt,"f∈C[a,b]={f:f为定义在[a,b]上的连续函数}是从C[a,b]到自身的线性算子,微分算子是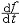 从 从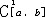 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 ={f:f为定义在[a,b]上具有一阶连续导数的连续函数}到C[a,b] 的线性算子。线性算子是线性泛函分析研究的基本对象之一,若X、Y为线性赋范空间,则可利用线性关系简化对连续性的讨论,此外,有限维空间上的线性算子必定连续,并且对线性算子来说,其连续性与有界性是等价的。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条