1) addition for bionomial and Poisson distribution


二项分布与Poisson分布的可加性
2) Poisson distribution


Poisson分布
1.
Multinomial distribution and multi-Poisson distribution;


多项分布与多元Poisson分布
2.
Optimizing order strategies of twoechelon retailer system with Poisson distributions;


基于Poisson分布需求的两级零售系统最优订货策略
3.
Several kind of estimates of Poisson distribution s parameter;


Poisson分布参数的几种估计
3) Poisson-Geometric distribution


Poisson-Geometric分布
4) Poisson-Geomtric distribution


Poisson-Geomtric分布
5) Poisson-Gumbel distribution


Poisson-Gumbel分布
6) Poisson type distribution


Poisson型分布
1.
It is proved in this parper that population X of nonsingula distribution with EX 2<∞ is of Poisson type distribution P(λ,α,1) if and only if the statistic T 2-T 1 has constant regression on T 1 ,where T 1==1n∑ni=1 X i is sample mean and T 2=1n-1∑ni=1(X i-) 2 is sample variance.
证明了满足EX2 <∞的具有非退化分布的母体X服从Poisson型分布P(λ ,α ,1)的充要条件是T2 -T1关于T1有常回归 ,其中T1= X =1n ∑ni =1Xi,T2 =1n - 1∑ni=1(Xi- X) 2 分别为子样均值和子样方
补充资料:二项分布
| 二项分布 binomial distribution 概率论中最常用的一种离散型概率分布。若随机变量遵从二项分布,则这个随机变量只取有限个值,即取0,1,2,…,n共n+1个整数值,取k值的概率为 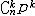 (1-p)n-k(k=0,1,2,…,n; (1-p)n-k(k=0,1,2,…,n;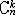 = =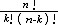 )。记二项分布为B(n,p)。因为 )。记二项分布为B(n,p)。因为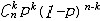 恰好是〔(1-p)+p〕n的二项式展开的第k+1项,所以二项分布由此得名。从不合格率为p的产品中独立地抽取n个产品(每次抽一个,抽取后又放回),其中恰有k个不合格品的概率就是 恰好是〔(1-p)+p〕n的二项式展开的第k+1项,所以二项分布由此得名。从不合格率为p的产品中独立地抽取n个产品(每次抽一个,抽取后又放回),其中恰有k个不合格品的概率就是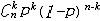 ,所以这n个产品中不合格品数是一个随机变量,它遵从二项分布。类似的例子在生产实践和科学实验中是常见的,将这类问题模型化,假设每一次试验只有两个可能结果:事件A出现或者不出现,A出现的概率为p,不出现的概率为1-p。这种只有两个可能结果的随机试验就称为伯努利试验,将这种试验独立地重复进行n次所组成的随机试验称为n重伯努利试验,其中事件A出现的次数Z是一个服从二项分布B(n,p)的随机变量。二项分布有两个参数n和p,n代表试验的总次数,p代表每次试验事件A出现的概率。二项分布B(n,p)的数学期望为np,方差为np(1-p)。当p固定,n充分大时,二项分布B(n,p)近似于正态分布,当p很小而n较大时,二项分布也可以用泊松分布来近似。 ,所以这n个产品中不合格品数是一个随机变量,它遵从二项分布。类似的例子在生产实践和科学实验中是常见的,将这类问题模型化,假设每一次试验只有两个可能结果:事件A出现或者不出现,A出现的概率为p,不出现的概率为1-p。这种只有两个可能结果的随机试验就称为伯努利试验,将这种试验独立地重复进行n次所组成的随机试验称为n重伯努利试验,其中事件A出现的次数Z是一个服从二项分布B(n,p)的随机变量。二项分布有两个参数n和p,n代表试验的总次数,p代表每次试验事件A出现的概率。二项分布B(n,p)的数学期望为np,方差为np(1-p)。当p固定,n充分大时,二项分布B(n,p)近似于正态分布,当p很小而n较大时,二项分布也可以用泊松分布来近似。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条