1) bounded variation functin class


有界变差函数类
2) strongly bounded varition function


强有界变差函数
3) bounded variation function


有界变差函数
1.
It is found that the monotone sequence is colsely related to it,and very similar with the bounded variation functions,and reach the conclusion as follows: the class of bounded sequence the class of convergencal sequence the bounded variation sequence the bounded monotone sequence.
本文主要对囿变数列的特征作一些探讨,我们发现:它与单调数列关系密切,而且与有界变差函数十分类似,并得出如下关系:有界数列类收敛数列类囿变数列单调有界数列。
2.
In this paper,we give the relation between the class H~ω of function and the class of bounded variation function,and generalize the results of Torriani.
给出函数类Hω和有界变差函数类BV之间的关系,推广了Torriani的结果。
3.
We study the approximation of Szasz-Bézier Operaters within [0,∞) for functions of bounded variation function f,and obtain an accurate estimate on the rate of convergence of this type.
对有界变差函数f的Szasz-Bézier算子在区间[0,∞)上的收敛阶进行估计。
4) bounded variation


有界变差函数
1.
There by the concepts such as bounded variation,the Riemann-stieltjes integral are extended to the locally convex space.
把向量值正则函数推广到了局部凸空间,得到了局部凸空间中向量值正则函数在s(0,1)的有界性,同时,把有界变差函数及Riemann-Stieltjes积分推广到了局部凸空间。
2.
The consepts such as bounded variation,the Riemann-Stieltjes integrl are extended to the locally convex space.
把实变函数中的有界变差函数推广到了局部凸空间中,同时,把Riemann-Stieltjes积分推广到了局部凸空间中向量值函数,得到了局部凸空间中向量值函数Riemann-Stieltjes积分的一些非常有价值的性质。
5) function of bounded variation


有界变差函数
1.
The problems of approximation by Euler means of Fourier series for the derivable function and function of bounded variation are studied, and the degrees of approximation are estimated.
研究Fourier 级数的Euler 平均对可导函数及有界变差函数的逼近,估计了逼近
2.
In this paper three stage function of bounded variation in sequence space λ is defined, and two of its necessary and sufficient conditions are given.
将λ-二级有界变差函数推广至λ-三级有界变差函数,并给出了它的2个充分必要条
3.
The denition of function of bounded variation is firstly given and it is then proved that monotonous functions of some kind of discontinuity and Lipchitz functions are functions of bounded variation.
文中给出有界变差函数的定义,并证明至多有可去间断点的单调函数和满足利普希茨条件的函数都是有界变差函数;建立了有界变差函数的小波级数的部分和的收敛性与收敛速度,并得出至多有可去间断点的单调函数与满足利普希茨条件的函数的小波级数的部分和的收敛性和收敛速度的推论。
6) function of Φ-bounded variation


Φ-有界变差函数
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 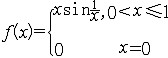 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条