1) separable metric space
可分度量空间
1.
The authors discuss some relations between the dimensions of the domain and the range of a continuous mapping and give the description of separable metric space in special sequence.
用特殊的复盖序列刻划可分度量空间的维数，并证明两个结果。
2) metrizable spaces
可度量空间
3) locally separable metric space
局部可分度量空间
1.
To give characterizations of the sequentially quotient,π-images and the sequentially covering, π-images of locally separable metric spaces in the notion of sieve and the following has.
利用筛的概念给出了局部可分度量空间的序列商象及序列覆盖π象的内在刻画,证明了空间是X局部可分度量空间的序列商(序列覆盖)π象当且仅当具X有可数纤维的cs* (cs)筛构成的点星网。
2.
In this paper, we have given an intemal depiction of closed S images of locally separable metric spaces.
给出局部可分度量空间闭S映象的一些内部刻划 ,证明了空间X是局部可分度量空间的闭S映象 ,当且仅当X是Fr啨ｃｈｅｔ空间且具有由可分子空间组成的σ 局部有限k 网 ,当且仅当X具有由可分子空间组成的σ 局部有限Fr啨ｃｈｅｔ拟基。
3.
In this paper the sequence-covering locally countable images of locally separable metric spaces are characterized.
本文给出了局部可分度量空间的序列复盖局部可数象的刻画。
4) locally separable metric spaces
局部可分度量空间
1.
In this paper the compact-covering ss-images and the compact-covering quotient compact ss-images of locally separable metric spaces are given.
给出了局部可分度量空间的紧覆盖ss-象及紧覆盖商紧ss-象的刻划。
2.
Some propositions about the quotient s-images of metric spaces and locally separable metric spaces are discussed.
对度量空间和局部可分度量空间的商s象进行了讨论。
5) sn-metrizable spaces
sn可度量空间
1.
Notes on sn-metrizable spaces;
关于sn可度量空间的注记
6) g-metrizable spaces
g-可度量空间
1.
In this paper,the relations between metrizable spaces and Ν-spaces or g-metrizable spaces are established by sequence-covering stratified strong compact mappings.
本文利用序列覆盖分层强紧映射,建立了Ν-空间,g-可度量空间与特定的度量空间的关系,这是对Alexandroff的部分问题的肯定回答。
2.
In the second part, the ralations between metrizable spaces and g-metrizable spaces are established by weak-open mapping.
第二部分利用弱开映射，建立了g-可度量空间与度量空间之间的关系，得到了对度量空间弱开k-映射的一些等价刻画并证明了度量空间、g-可度量空间、sn-可度量空间、N-空间在弱开、闭映射下保持。
补充资料：度量空间
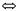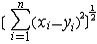| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…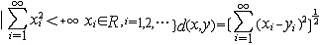）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条