1) multimode Schrdinger-cat light field
多模薛定谔猫态光场
2) Multimode Schodinger-cat state light field
多模薛定谔猫态
3) multimode Schr o ¨dinger cat state light fields
多模薛定谔猫(Schro¨dinger-cat)态光场
4) Multimode amplitude Schro ¨dinger-Cat state
多模振幅薛定谔猫态
5) two-mode Schrodinger's cat states
双模薛定谔猫态
6) Schrdinger cat states
薛定谔猫态
1.
The squeezing of angular momentum and its evolutions in atomic Schrdinger cat states;
原子薛定谔猫态中角动量的压缩及其时间演化
2.
,Schrdinger cat states.
提出了一种制备相干态的叠加态 ,即薛定谔猫态的方案 。
补充资料：薛定谔方程
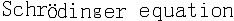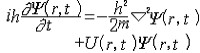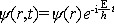薛定谔方程 E.薛定谔提出的量子力学基本方程 。建立于 1926年。它是一个非相对论的波动方程。它反映了描述微观粒子的状态随时间变化的规律，它在量子力学中的地位相当于牛顿定律对于经典力学一样，是量子力学的基本假设之一。设描述微观粒子状态的波函数为Ψ（r，t），质量为m的微观粒子在势场U（r，t）中运动的薛定谔方程为  。在给定初始条件和边界条件以及波函数所满足的单值、有限、连续的条件下，可解出波函数Ψ（r，t）。由此可计算粒子的分布概率和任何可能实验的平均值（期望值）。当势函数U不依赖于时间t时，粒子具有确定的能量，粒子的状态称为定态。定态时的波函数可写成 式中Ψ（r）称为定态波函数，满足定态薛定谔方程 ，这一方程在数学上称为本征方程，式中E为本征值，是定态能量，Ψ（r）又称为属于本征值E的本征函数。量子力学中求解粒子问题常归结为解薛定谔方程或定态薛定谔方程。薛定谔方程广泛地用于原子物理、核物理和固体物理，对于原子、分子、核、固体等一系列问题中求解的结果都与实际符合得很好。 薛定谔方程仅适用于速度不太大的非相对论粒子，其中也没有包含关于粒子自旋的描述。当计及相对论效应时，薛定谔方程由相对论量子力学方程所取代，其中自然包含了粒子的自旋。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条