1) Schrdinger-cat-like states
类薛定谔猫态
1.
In this paper, soliton squeezing in a nonlinear Mach-Zehnder interferometer is discussed by means of time-dependent Hartree approximation <(Δ)~2>min)～<>1/3), and the generation of Schrdinger-cat-like states for quantum foundamental solitons in optical fibers is also investigated.
利用与时间有关的Hartree近似法证明借助非线性Mach-Zehnder干涉仪可以得到光孤子的光子数压缩态<(Δ^N)2>min～<^N>1/3,并且指出在一些特定时刻光纤孤子会呈现出类薛定谔猫态(Schr dinger-cat-likestates)。
2) Schrdinger cat states
薛定谔猫态
1.
The squeezing of angular momentum and its evolutions in atomic Schrdinger cat states;
原子薛定谔猫态中角动量的压缩及其时间演化
2.
,Schrdinger cat states.
提出了一种制备相干态的叠加态 ,即薛定谔猫态的方案 。
3) Schrdinger cat states
薛定谔猫态
1.
In the interaction system of single-mode cavity and moving-mirror,how to prepare entangled states of single-mode cavity,a moving-mirror, and Schrdinger cat states of the cavity are described via selecting appropriate interaction time.
描述了在腔场与可移动镜子相互作用系统中 ,适当选择作用时间 ,可以制备单模腔场与镜子的纠缠态 ,或腔场的薛定谔猫态 ;通过调节腔场的长度、圆频率 ,以及镜子的质量、振动频率等宏观物理量 ,可以获得不同的量子态 。
2.
We have found there is higher power squeezing for real and imaginary Schrdinger cat states.
发现实虚薛定谔猫态存在高阶压缩效应，并把实虚薛定谔猫态的高阶非经典性质与偶奇相干态作了比
4) Schrdinger cat state
薛定谔猫态
1.
Evolution of field entropy in a system of Schrdinger cat state light field interacting with two moving entangled atoms;
运动纠缠双原子与薛定谔猫态光场相互作用系统的场熵演化
2.
A scheme is proposed for teleportation of Schrdinger cat state of cavity field by using the non maximally entangled atom cavity states via the J C model with large detuning.
提出了利用这个原子与光场的非最大纠缠态 ,通过大失谐的J C模型传送腔场的薛定谔猫态的方
5) Schro ¨dinger cat state
薛定谔猫态
1.
In this paper,the distance between density operators has been used to examine that the field evolves periodically to the Schro ¨dinger cat state in the nonlinear (intensity dependent) Jaynes Cummings model for large initial coherent state(n1).
本文采用密度算符间的距离论证了非线性（强度相关）ＪａｙｎｅｓＣｕｍｍｉｎｇｓ模型在初始相干光场很强的条件下光场周期地演化为薛定谔猫态，且薛定谔猫态的特性取决于原子的初态
6) squeezing Schrodinger cat state
压缩薛定谔猫态
1.
The studies showed: Considered the influence of the infirmness coupling effect in a mesoscopic capacitor, the mesoscopic LC circuit would evolve into squeezing Schrodinger cat state from Schrodinger cat state.
研究结果表明:考虑介观电 容器弱耦合效应的影响,介观LC电路将由初始的薛定谔猫态演化到压缩薛定谔猫态。
补充资料：薛定谔方程
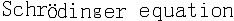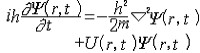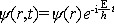薛定谔方程 E.薛定谔提出的量子力学基本方程 。建立于 1926年。它是一个非相对论的波动方程。它反映了描述微观粒子的状态随时间变化的规律，它在量子力学中的地位相当于牛顿定律对于经典力学一样，是量子力学的基本假设之一。设描述微观粒子状态的波函数为Ψ（r，t），质量为m的微观粒子在势场U（r，t）中运动的薛定谔方程为  。在给定初始条件和边界条件以及波函数所满足的单值、有限、连续的条件下，可解出波函数Ψ（r，t）。由此可计算粒子的分布概率和任何可能实验的平均值（期望值）。当势函数U不依赖于时间t时，粒子具有确定的能量，粒子的状态称为定态。定态时的波函数可写成 式中Ψ（r）称为定态波函数，满足定态薛定谔方程 ，这一方程在数学上称为本征方程，式中E为本征值，是定态能量，Ψ（r）又称为属于本征值E的本征函数。量子力学中求解粒子问题常归结为解薛定谔方程或定态薛定谔方程。薛定谔方程广泛地用于原子物理、核物理和固体物理，对于原子、分子、核、固体等一系列问题中求解的结果都与实际符合得很好。 薛定谔方程仅适用于速度不太大的非相对论粒子，其中也没有包含关于粒子自旋的描述。当计及相对论效应时，薛定谔方程由相对论量子力学方程所取代，其中自然包含了粒子的自旋。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条