1) p-stress-energy tensor
p-应力-能量张量
2) p stressenergy tensor
p应力能量张量
3) p stress energy tensor
p-应力能量张量
4) stress-energy tensor
应力能量张量
1.
This paper gives a definition of F-stress-energy tensor with p-forms on the complete simply connected Riemannian mainfolds with the bounded negative sectional curvature,and extends F-harmonic maps Liouville type theorem to the general case of F-stress-energy tensor with p-form on vector bundle satisfying the law of conservation.
在此建立了具有有界的负截面曲率的完备单连通黎曼流形上p-形式的F-应力能量张量,并将F-调和映射的Liouville型定理推广到F-应力能量张量满足守恒律的向量丛值p-形式的一般情形,从而得到这类p-形式的一些消没定理。
5) energy-momentum stress
能量应力张量
1.
In this paper we turn out the coherent-state expression of energy-momentum stress tensor in two dimensional Schwarzschild black holes.
讨论了一个二维黑洞的能量应力张量的相干态表示，并将这样得到的结果与已有的结果进行比较和讨论。
6) F-stress-energy tensor
F-应力能量张量
补充资料：应力
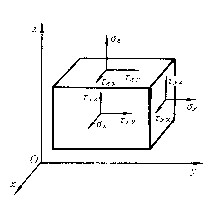
| 应力 stress 由载荷、温度、湿度等因素引起物体内部某点处截面内力的集度。其大小和方向决定于所考虑点的位置和截面方向。若过某点任一截面微元ΔS上的内力合力为ΔF，则该点在此截面上的应力σ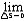＝  ΔF／ΔS 。此应力在截面法线方向的分量称法向应力，在截面内的分量称剪应力。物体内某点不同方向截面上的应力情况称该点的应力状态。物体内任一点的应力状态可由过该点3个相互垂直平面上的9个应力分量σx、τxy、τxz ,σy、τyx、τyz ,σz、τzx、τzy表示（见图）。其中τxy＝τyx ,τyz＝τzy ,τzx＝τxz，故只有6个应力分量是独立的。过该点任一平面上的应力在x、y、z轴上的分量为：X＝lσx＋mτxy＋nτxz ，Y＝lτyx＋mσy＋nτyz ，Z＝lτzx＋mτzy＋nσz ，式中l、m、n为所考虑平面的法线同x、y、z轴夹角的方向余弦。应力是确定材料或构件是否会破坏的一个重要力学参量。
|
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条