1) degree of Integral function


整函数级
1.
In this paper,we analyze the definition of degree of Integral function,give some ways of the definition,and obtain some conclusions by comparing the
文章对整函数级定义进行了分析,给出了几种定义方式,对这些方式作了比较并得出了一些结论。
3) The Proximate Order of Entire Function


整函数的近似级
4) lower logarithmic degree


整函数的下对数级
5) function series


函数级数
1.
It is of great importance to study the analytic quality of sum function in function series.
对于函数级数,研究其和函数的解析性质很重要,但函数级数必须具有一致收敛性,而判断函数级数的一致收敛性往往是比较困难的。
6) integral function


取整函数
1.
Some probabilistic properties of integral function are discussed and some decomposition methods of non-negative random variable are proved.
通过讨论取整函数的几个概率性质,证明了对非负随机变量的取整函数分解方法,并把这种分解方法用于纺织纤维加工工艺中纱条牵切前后纤维长度分布之间关系的分析中。
2.
The paper discusses several analytic characters and the extensive application of the integral function and fraction parts of functions,which have the differentiation with contact.
取整函数与小数部分函数既相互联系又有区别,各有一些独特的性质,在数学及生活中有着较广泛的应用。
补充资料:整函数
| 整函数 integral function 在整个复平面上处处解析的函数。整函数总可以在原点 展开成泰勒级数:  ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如 ,它在全平面收敛,整函数以∞点为唯一的孤立奇点,它在∞点的罗朗展式与它在原点的泰勒展式有一样的形式。当∞点是整函数的可去奇点时,这个整函数只能是常数,这就是著名的刘维尔定理,通常表述为“有界整函数必为常数”。利用这一定理可以得到代数基本定理的简单证明。当∞点是整函数的n阶极点时,这个整函数是一个n次多项式 ,也就是它的泰勒展式(或罗朗展式)只有有限多项。当∞点是整函数的本性奇点时,这个整函数的泰勒展式一定有无限多项,这类整函数称为超越整函数。由代数基本定理知道n次多项式一定有n个零点(也就是根),它总可以分解为n个一次因式的积,对于超越整函数,它可能有无限多个零点 ,比如sinπz就以全体整数为其零点集,也有的超越整函数没有零点,如ez就处处不为零,一般来说,没有零点的超越整函数总可以表成eg(z)的形式,此处g(z)也是一个整函数,而有无限多个零点的超越整函数f(z)也有一个因子分解式 ;形如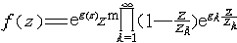 ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( ,其中g(z)是整函数,0是m阶零点,zk是非零零点集,gk( )是 )是 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk 的多项式,这是魏尔斯托拉斯因子分解定理。超越整函数还有一个重要性质:若f(z)是超越整函数,则对任意复数A(包括A=∞),存在点列{zk },使zk  ∞(k ∞(k ∞)而有f(zk) ∞)而有f(zk) A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 A。这一结果有一个更精确的发展:对超越整函数f(z),最多除去一个值(称为例外值)外,对所有其他的复数v值(v≠∞),f(z)-v都有无穷多个零点(毕卡定理)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条