1) Wiener equation


维纳方程
1.
The proof of the new algorithm was also presented, which showed that its optimal weight vector was the solution of generalized Wiener equation.
从信号前后时刻相关性角度出发,提出了一种新的快速自适应滤波算法,并证明了其最优权值是一种广义的维纳方程解。
2) Wiener Hopf equation


维纳霍夫方程
3) Wiener-Hopf equation


维纳-霍甫夫方程
4) Navier-Stokes equation


纳维尔斯托克斯方程
5) Navier-Stokes equations


纳维斯托克斯方程
1.
Overseeing mathematic model, Reynolds Average Navier-Stokes equations is used for basic control equations, SST k ?ωturbulence model is used for closure, and Volume of Fluid scheme is used to capture information of two phases.
数学模型中,基本控制方程使用雷诺时均纳维斯托克斯方程,采用SSTk?ω湍流模型封闭方程,并使用流体体积法捕捉气液两相信息。
6) Navier-Stokes equations


纳维尔-斯托克斯方程
补充资料:纳维-斯托克斯方程
| 纳维-斯托克斯方程 Navier-Stokes equations 描述粘性不可压缩流体动量守恒的运动方程。简称N-S方程。因1821年由C.-L.-M.-H.纳维和1845年由G.G.斯托克斯分别导出而得名。在直角坐标系中,可表达为 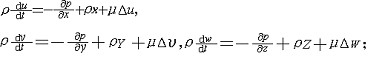 其矢量形式为 其矢量形式为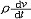 =-Ñp+ρF+μΔv,式中ρ为流体密度,p为压强,u(u,v,w)为速度矢量,F(X,Y,Z)为作用于单位质量流体的彻体力,Ñ为哈密顿算子 ,Δ为拉普拉斯算子。后人在此基础上又导出适用于可压缩流体的N-S方程。N-S方程反映了粘性流体(又称真实流体)流动的基本力学规律,在流体力学中有十分重要的意义。它是一个非线性偏微分方程,求解非常困难和复杂,目前只有在某些十分简单的流动问题上能求得精确解;但在有些情况下,可以简化方程而得到近似解。例如当雷诺数Re =-Ñp+ρF+μΔv,式中ρ为流体密度,p为压强,u(u,v,w)为速度矢量,F(X,Y,Z)为作用于单位质量流体的彻体力,Ñ为哈密顿算子 ,Δ为拉普拉斯算子。后人在此基础上又导出适用于可压缩流体的N-S方程。N-S方程反映了粘性流体(又称真实流体)流动的基本力学规律,在流体力学中有十分重要的意义。它是一个非线性偏微分方程,求解非常困难和复杂,目前只有在某些十分简单的流动问题上能求得精确解;但在有些情况下,可以简化方程而得到近似解。例如当雷诺数Re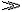 1时,绕流物体边界层外 ,粘性力远小于惯性力 ,方程中粘性项可以忽略,N-S方程简化为理想流动中的欧拉方程( 1时,绕流物体边界层外 ,粘性力远小于惯性力 ,方程中粘性项可以忽略,N-S方程简化为理想流动中的欧拉方程(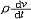 =-Ñp+ρF);而在边界层内,N-S方程又可简化为边界层方程,等等。在计算机问世和迅速发展以后,N-S方程的数值求解才有了很大的发展。 =-Ñp+ρF);而在边界层内,N-S方程又可简化为边界层方程,等等。在计算机问世和迅速发展以后,N-S方程的数值求解才有了很大的发展。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条