1) Navier-Stokes equation


纳维-斯托克斯方程
1.
The model function of wake vortexes for the lifting surface method,the numerical treatment of Kutta condition on blade trailing for panel approach,and the numerical procedure and mathematical models of matching computation for Navier-Stokes equation method are discussed and the application examples of viscous modification,calculation of two-phase flow around foils and development of new blade.
论述了船用螺旋桨理论设计与计算研究的进展;讨论了升力面理论方法中尾涡模式函数,面元法中的随边库塔条件的数值处理,以及纳维-斯托克斯方程方法中流域计算匹配的数值方法;给出了相关理论方法在螺旋桨水动力性能黏性修正、翼剖面二相流水动力计算和新型螺旋桨叶剖面设计开发研究中的应用实例。
2.
By using spectral collection methods on the Navier-Stokes equation,we can omit the pressure item and consider the diffusion,advection and additional force as an integer to deal with.
该方法将流体运动从通常的实空间转换到谱空间进行运算,对纳维-斯托克斯方程采用谱配置法进行求解,从而直接消去了压力项,并将原方程中的扩散、平流、外力项做为一个整体用简单的代数运算来进行处理,避免了把纳维-斯托克斯方程拆成几项分别求解带来的误差和用迭代法求解泊松方程的繁复运算,大大降低了实时流体模拟过程中的运算量。
2) navier stokes equation


纳维-斯托克斯方程
3) Navier-Stokes equations


纳维-斯托克斯方程
1.
Navier-Stokes equations is a admittedly physically-based fluid dynamics model.


纳维-斯托克斯方程是描述流体运动的基础物理模型。
4) Navier-Stokes equation


纳维尔斯托克斯方程
5) Navier-Stokes equations


纳维斯托克斯方程
1.
Overseeing mathematic model, Reynolds Average Navier-Stokes equations is used for basic control equations, SST k ?ωturbulence model is used for closure, and Volume of Fluid scheme is used to capture information of two phases.
数学模型中,基本控制方程使用雷诺时均纳维斯托克斯方程,采用SSTk?ω湍流模型封闭方程,并使用流体体积法捕捉气液两相信息。
6) Navier-Stokes equations


纳维尔-斯托克斯方程
补充资料:纳维-斯托克斯方程
| 纳维-斯托克斯方程 Navier-Stokes equations 描述粘性不可压缩流体动量守恒的运动方程。简称N-S方程。因1821年由C.-L.-M.-H.纳维和1845年由G.G.斯托克斯分别导出而得名。在直角坐标系中,可表达为 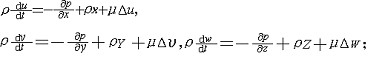 其矢量形式为 其矢量形式为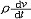 =-Ñp+ρF+μΔv,式中ρ为流体密度,p为压强,u(u,v,w)为速度矢量,F(X,Y,Z)为作用于单位质量流体的彻体力,Ñ为哈密顿算子 ,Δ为拉普拉斯算子。后人在此基础上又导出适用于可压缩流体的N-S方程。N-S方程反映了粘性流体(又称真实流体)流动的基本力学规律,在流体力学中有十分重要的意义。它是一个非线性偏微分方程,求解非常困难和复杂,目前只有在某些十分简单的流动问题上能求得精确解;但在有些情况下,可以简化方程而得到近似解。例如当雷诺数Re =-Ñp+ρF+μΔv,式中ρ为流体密度,p为压强,u(u,v,w)为速度矢量,F(X,Y,Z)为作用于单位质量流体的彻体力,Ñ为哈密顿算子 ,Δ为拉普拉斯算子。后人在此基础上又导出适用于可压缩流体的N-S方程。N-S方程反映了粘性流体(又称真实流体)流动的基本力学规律,在流体力学中有十分重要的意义。它是一个非线性偏微分方程,求解非常困难和复杂,目前只有在某些十分简单的流动问题上能求得精确解;但在有些情况下,可以简化方程而得到近似解。例如当雷诺数Re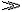 1时,绕流物体边界层外 ,粘性力远小于惯性力 ,方程中粘性项可以忽略,N-S方程简化为理想流动中的欧拉方程( 1时,绕流物体边界层外 ,粘性力远小于惯性力 ,方程中粘性项可以忽略,N-S方程简化为理想流动中的欧拉方程(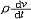 =-Ñp+ρF);而在边界层内,N-S方程又可简化为边界层方程,等等。在计算机问世和迅速发展以后,N-S方程的数值求解才有了很大的发展。 =-Ñp+ρF);而在边界层内,N-S方程又可简化为边界层方程,等等。在计算机问世和迅速发展以后,N-S方程的数值求解才有了很大的发展。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条