1) Partial derivative estimation


偏导数估计
2) derivative estimation


导数估计
1.
The method of Bessel derivative estimation has been improved and presented different from ref[1] in this paper,in which a correcting strategy is used to get higher estimation precision.
文章从另一思想角度实现了文献中提出的新方法,即利用误差事后估计的方法对Bessel导数估计方法进行改进,提高了导数估计值的精度。
3) unbiased estimator


不偏估计数
4) differential kernel estimation


导数核估计
5) unbiased parameter estimation


无偏参数估计
6) integer frequency offset estimation


整数倍频偏估计
补充资料:偏导数
| 偏导数 partial derivative 二元函数z=f(x,y)沿坐标轴方向的方向导数(或沿坐标轴方向的变化率)。即把z=f(x,y)中的一个自变量y看作常数,于是z=f(x,y)就成为关于x的一元函数,给x以改变量Δx,则有z关于x的(偏)改变量Δxz=f(x+Δx,y)-f(x,y),如果极限(  存在且有限,就称此极限为二元函数 z =f( x,y )在 P(x,y)点关于x的偏导数,记作 存在且有限,就称此极限为二元函数 z =f( x,y )在 P(x,y)点关于x的偏导数,记作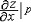 ,或 ,或 (x,y),类似地有 (x,y),类似地有
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |