1) fractal order
分形阶数
2) fractional order linear time-invariant system
分数阶线形定常系统
1.
A new fractional order state observer of fractional order linear time-invariant system was proposed,which is the generalization of classical integer order state observer based on fractional calculus.
提出了一种新的基于分数阶线形定常系统的全维状态观测器,把传统的整数阶状态观测器的阶次推广到分数领域,给出了分数阶线形定常系统全维状态观测器的一种设计方案以及综合算法,同时给出了具体设计步骤。
3) differential order
微分阶数
4) fractional-order
分数阶
1.
Designing synchronization schemes for a fractional-order hyperchaotic system;
一个分数阶新超混沌系统的同步
2.
Adaptive synchronization of the fractional-order unified chaotic system
分数阶统一混沌系统的自适应同步
5) fractional order
分数阶
1.
Study on a class of chaotic systems with fractional order;
一类分数阶混沌系统的研究
2.
Controlling projective synchronization in coupled fractional order chaotic Chen system;
两个耦合的分数阶Chen系统的混沌投影同步控制
3.
Study on the critical chaotic system with fractional order and circuit experiment;
分数阶临界混沌系统及电路实验的研究
6) difference order
差分阶数
1.
The time series model of Guangxi s GDP is established using comprehensively the method of judging the stationary time series process, using the method of unit root to test the difference order, and using the autocorrelation and partial autocorrelation functions graph to identify the autoregressive process of order (AR(p)) and sliding average process of order (MA(q)).
综合运用了判别时间序列平稳性的方法,利用单位根方法检验时间序列的差分阶数;利用自相关函数图和偏相关函数图判别时间序列模型的自回归阶数(AR(p))和滑动平均阶数(MA(q)),建立广西GDP的时间序列模型。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 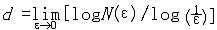 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条