1) algebraic topology
代数拓扑
1.
Based on the assumptions of a single channel between two nodes and no capacity in nodes, the algebraic topology theory can be used to construct a frame for analyzing longitudinal dispersion through fractured rock network.
揭示一个基于代数拓扑理论的裂隙网络中物质弥散模型，还给出了应用于网络中的对流扩散的对应性原理的证明。
2.
A fracture network model based on algebraic topology theory has been developed to study fluid flow in the fracture dominant media.
提出一个基于代数拓扑理论的裂隙网络中流体分布的离散模型。
2) algebraical topology
代数拓扑
1.
Method of algebraical topology is used in logic synthesis;
代数拓扑方法应用于逻辑综合
2.
Method of algebraical topology used in logic synthesis attained least covering, and in order to avoid audaciousness arising,auducious problem was discussed necessarily.
代数拓扑方法用于逻辑综合得到最小覆盖 ,为了避免可能出现冒险 ,需要进行冒险问题的讨
3) topological algebra
拓扑代数
4) topological BCI-algebras
拓扑BCI代数
5) fuzzy topological algebra
fuzzy拓扑代数
6) algebraic topology
代数拓扑学
补充资料：代数拓扑
| 代数拓扑 algebraic topology 拓扑学中主要用代数工具解决问题的分支。它的前身是组合拓扑，组合拓扑的奠基人是H.庞加莱，1895年他建立了单纯同调群即可三角剖分的空间（多面体）的同调群，引进了重要的拓扑不变量贝蒂数及挠系数。J.W.亚历山大在1915年证明了贝蒂数和挠系数是同胚不变量，单纯同调群是同胚不变量。同时庞加莱还引进了复形的基本群。1904年他给出了庞加莱猜想，即每个单连通的闭的可定向的三维流形同胚于三维球面 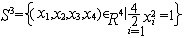 ，这个猜想后被推广为每个单连通的闭的n维流形，如果具有n维球S的贝蒂数和挠系数，它就同胚于S。庞加莱猜想尚未被证明。推广了的庞加莱猜想，对于n≥5的情形，为S.斯梅尔于1961年证明，对n＝4的情形，为M.H.弗里德曼于1981年所证明。庞加莱是企图利用同调群和基本群对三维流形进行同胚分类，但亚历山大在1919年指出存在不同胚的三维流形，它们有同构的同调群和基本群。20世纪20年代S.莱夫谢茨和亚历山大发展了同调论，得到了霍普夫不变量，证明了莱夫谢茨不动点定理，亚历山大对偶定理。20世纪初引进了一般空间的同调群。1932年E.切赫上同调群产生。1944年S.艾伦伯格定义了奇异同调群且用艾伦伯格- 斯廷罗德公理把各种同调群统一起来，建立了同调理论。在同伦论方面W.赫维茨定义了同伦群。J.H.C.怀特赫德把研究对象推广到CW复形。1947年N.E.斯廷罗德在障碍理论中定义了斯廷罗德平方运算。1951年 J.-P.塞尔对纤维丛引进了谱序列，在同伦群的计算方面取得不少成就。此外纽结问题也进一步发展成为思维合痕和嵌入问题。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条