1) hyperbolic differential equation


双曲微分方程
1.
This paper discusses the oscillation of solutions for a kind of neutral hyperbolic differential equations.
研究了一类中立型双曲微分方程解的振动性 ,获得了在齐次 Dirichlet,Neumann和 Robin边值条件下所有解振动的充分条
2.
By establishing a functional differential inequality and using a generalized Riccati transformation,some sufficient conditions are obtained for the oscillation of solutions of certain neutral delay hyperbolic differential equation
通过建立泛函微分不等式,利用广义Riccati变换,研究了一类中立型时滞双曲微分方程解的振动性。
2) hyperbolic equation


双曲微分方程
1.
Oscillation criteria for nonlinear neutral hyperbolic equations with continuously distributed delays;
具有连续分布时滞的非线性中立型双曲微分方程解的振动性
2.
An averaging technique is used to study the forced oscillation of nonlinear hyperbolic equations with a distributed deviating argument.
使用平均值技巧 ,把多维问题变为一维的微分方程或微分不等式的振动问题 ,研究具有分布偏差变元的双曲微分方程解的强迫振动性 。
3) hyperbolic PDEs


双曲偏微分方程
1.
By means of interpolating wavelets theory ,we construct an adaptive algorithm to solve linear and nonlinear hyperbolic PDEs.
借助于插值小波理论 ,构造了用插值小波求解一维双曲偏微分方程的自适应算法 。
4) hyperbolic differential equation


双曲型微分方程
1.
Some necessary and sufficient conditions for the oscillation of solutions of delay hyperbolic differential equations are obtained.
建立了一类时滞双曲型微分方程解的振动充要条件,揭示了这类双曲方程与相应泛函微分方程解的振动的等价性。
2.
By using a generalized Riccati transformation, some sufficient conditions are established for the oscillation of solutions of delay hyperbolic differential equations of the form ~2 t~2u(x,t) =a(t)Δu(x,t)+sk=1a_k(t)Δ u(x,t-ρ_k)-mj=1q_j(x,t)u(x,t-σ_j), where (x,t)∈Ω×[0,∞)≡G, Ω is a bounded domain in R~N with a piecewise smooth boundary Ω and Δ is the Laplacian in Euclidean N-space R~N.
利用广义Riccati变换 ,建立了下列时滞双曲型微分方程 2 t2 u(x ,t) =a(t)Δu(x ,t) + sk =1ak(t)Δu(x ,t- ρk) - mj =1qj(x,t)u(x,t-σj)解的振动的若干充分条件 ,其中 (x ,t)∈Ω× [0 ,∞ )≡G ,Ω是RN中具有逐片光滑边界 Ω的有界区域 ,Δu(x ,t) = Nr=1 2 u(x ,t) x2r。
3.
In this paper,by using the characteristic equation,some forced oscillation of certain delay hyperbolic differential equations are obtained.
借助其特征方程 ,获得了一类时滞双曲型微分方程解的强迫振动的若干充分条
5) hyperbolic equation


双曲型微分方程
1.
This paper deals with the Cauchy problem for a hyperbolic equation of second order by transforming the problem into a system of integral equations,thus proving that the problem has differentiable solution under some conditions by using the iteration method.
研究了二阶双曲型微分方程沿着一组特征线的柯西问题 ,处理这个问题的方法是通过引入辅助函数 ,转化为求解积分方程组 ,并利用迭代法 ,证明了在一定条件下这个二阶双曲型微分方程的柯西问题有
2.
Deals with the Cauchy problem for a hyperbolic equation of second order v xx -h(x,y)k(y)v yy +a(x,y)v x+b(x,y)v y+c(x,y)v+f(x,y)=0.
研究了一类二阶双曲型微分方程 vxx-h( x,y) k( y) vyy+ a( x,y) vx+ b( x,y) vy+ c( x,y) v+ f ( x,y) =0的柯西问题解的存在性 。
6) hyperbolic differential equations


双曲型微分方程
1.
Sufficient conditions are obtained for oscillation of solutions of a nonlinear delayed hyperbolic differential equations 2ut 2=a(t)Δu+si=1a i(t)Δu(x,t-ρ i(t))-f(x,t,u)-kj=1g j(x,t,u(x,t-σ j)),(x,t)∈Ω×(0,∞) with u=0,(x,t)∈Ω× 0,∞).
给出具有非线性时滞的双曲型微分方程定解问题2ut2=a(t)Δu+si=1ai(t)Δu(x,t-ρi(t))-f(x,t,u)-kj=1gj(x,t,u(x,t-σj)),u=0,(x,t)∈Ω×〔0,∞),其中(x,t)∈Ω×(0,∞)的解振动的几个充分条件。
补充资料:双曲型偏微分方程
| 双曲型偏微分方程 hyperbolic type,partial differential equation of 描述振动或波动现象的偏微分方程。它的一个典型特例是波动方程 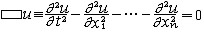 n=1时的波动方程 n=1时的波动方程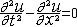 可用来描述弦的微小横振动,称为弦振动方程。这是最早得到系统研究的一个偏微分方程。 可用来描述弦的微小横振动,称为弦振动方程。这是最早得到系统研究的一个偏微分方程。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条