1) Homology group


同调群
1.
The further description on the structure of homology group with integral coefficients;


关于整同调群结构的进一步刻画
2.
Here we generalize the theory to the ring Z to compute 1-dimensional homology group of a given 2-complex with a combination of algebraic and graph-theoretic method.
文献[3]在有限域Z_2上描述了图G的“圈空间”,这里我们将此理论推广到一般环Z上用以计算给定2-复型的一维同调群,其中我们采用的方法是代数与图论相结合的方法。
3.
Some of homology groups in algebraic geometry are calculated.


对代数几何中一些同调群进行计算 ,给出A -S指数定理在四元数射影空间同调群上的一个应用 。
4) coherent generators


同调机群
1.
In this paper,the dynamic equivalent problem for multi-area interconnected power systems is analyzed and a distributed algorithm for identifying coherent generators is presented based on the real-time simulation algorithm.
本文研究了与市场条件相适应的区域互联电力系统发电机同调识别问题,基于经典的时域仿真算法,提出了一种子系统同调机群分布式识别方法。
2.
Based on principal component analysis (PCA), a new method to recognize the coherent generators of power system is proposed.
提出了一种基于主成分分析(principal component analysis,PCA)的电力系统同调机群分群识别方法。
5) group homology inverse


群同调逆
1.
(i,p)-homology inverse and group homology inverse are defined in this paper on categories of topologicalspace with base point.
在点标拓扑空间范畴中引进了(i,p)-同调逆和群同调逆的概念,并讨论了它们存在的条件和性质。
6) coherent generator groups


同调机群
1.
In this paper,the fuzzy clustering method is introduced to identify coherent generator groups in power system.
引入模糊聚类方法识别电力系统同调机群。
2.
A fuzzy clustering method for recognizing coherent generator groups in power system is proposed in this paper.
给出了一种能识别电力系统同调机群的模糊聚类方法。
补充资料:同调群
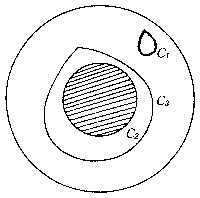
| 同调群 homology group 代数拓扑的概念。同调的直观解释如下:如图,在圆环中闭曲线C1是所围区域的边界,称为一维闭链C1同调于零;而C2、C3都不是自己所围区域的边界,称C2和C3均是不同调于零的闭链。但C2和C3合起来是共同所围区域的边界,则称一维闭链C2和C3同调。类似地可对各维闭链定义同调的概念。用同调这等价关系对各维闭链进行等价分类,就得到各维同调群,用它来刻画拓扑空间包含各维洞的情况。
H.庞加莱从1895年起为对同调概念进行一般讨论 ,引进了可剖分为复形的空间,从此产生了组合拓扑学。关于同调群的理论,就已成为代数拓扑的内容极其丰富的组成部分。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条