1) homology and co homology


同调与上同调群
2) cohomology groups


上同调群
1.
The information about the first Chern class makes the cohomology groups and homotopy groups of the configuration space worked out.
由此又算出了它的上同调群与同伦群。
3) cohomology
[kəuhə'mɔlədʒi]


上同调群
1.
The theory of homology and cohomology is very important in mathematics.


本文结合超代数上同调群的定义,研究得到了具有相伴单位元1的结合超代数的上同调群的一些较好的性质。
4) cohomology group


上同调群
1.
The cohomology group of holomorphic line bundles on Hopf manifolds;


Hopf流形上线丛的上同调群
2.
The present thesis is devoted to studying the second cohomology groups of modularLie superalgebras of Cartan type.
本文主要研究几类Cartan型模李超代数的二阶上同调群。
6) Hochschild cohomology group


Hochschild上同调群
1.
Hochschild cohomology groups of the hereditary algebras with three simple modules;


具有三个单模的有限维遗传代数的Hochschild上同调群
2.
Based on the minimal projective bimodule resolution constructed by Bardzell,the dimensions of all Hochschild cohomology groups ofΛ_d are calculated explicitly in terms of combinatorics.
设Λ_d是Fibonacci代数,基于对Bardzell极小投射双模分解的细致分析,用组合的方法清晰地计算了Fibonacci代数Λ_d的各阶Hochschild上同调群的维数。
3.
Based on the minimal pro- jective bimodule resolution constructed by Bardzell,the dimensions of all Hochschild cohomology groups of A are explicitly calculated.
设A是有限表示型遗传代数A=kQ的投射模范畴proj A上的根双模rad(-,-)所对应的拟遗传代数,基于Bardzell构造的极小投射双模分解,A的各阶Hochschild上同调群的维数被清晰地计算。
补充资料:同调群
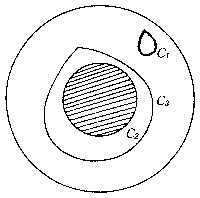
| 同调群 homology group 代数拓扑的概念。同调的直观解释如下:如图,在圆环中闭曲线C1是所围区域的边界,称为一维闭链C1同调于零;而C2、C3都不是自己所围区域的边界,称C2和C3均是不同调于零的闭链。但C2和C3合起来是共同所围区域的边界,则称一维闭链C2和C3同调。类似地可对各维闭链定义同调的概念。用同调这等价关系对各维闭链进行等价分类,就得到各维同调群,用它来刻画拓扑空间包含各维洞的情况。
H.庞加莱从1895年起为对同调概念进行一般讨论 ,引进了可剖分为复形的空间,从此产生了组合拓扑学。关于同调群的理论,就已成为代数拓扑的内容极其丰富的组成部分。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条