1) Euler and Laplace equations


欧拉方程与拉普拉斯方程
2) Laplace equation


拉普拉斯方程
1.
The 5-point finite analytic schemes for laplace equation in irregular domains;


非规则区域中拉普拉斯方程的有限分析5点格式
2.
Based on measuring rock core in lab and started from Laplace equation of capillary,This thesis presents the method of evaluating reservoir wettability using conventional logging data,which realizes continuous,quick and quantitative evaluation of reservoir wettability accordingly.
以岩心实验为基础,根据毛细管拉普拉斯方程,实现油层润湿性的连续、快速、定量评价。
3.
It is complicated and hard-controlled for beginner to solve the Laplace equation in the static electricity field.
在静电场中求解拉普拉斯方程,对初学者来说既复杂又难以掌握。
4) Laplace Equations


拉普拉斯方程
1.
Based on the solution of the Laplace Equations, a numerical procedure for generation of 2-D orthogonal body-fitted curvilinear coordinate system is developed in which the grid points on the boundary can be arbitrarily determined.
结果表明:该法以求解拉普拉斯方程组为基础,物理概念明确,且无需构造"合并"或"聚集"控制函数,使得方程离散简单,经验性因素降低;该法网格线与边界的正交性良好,可随意控制网格的疏密度,而且利用这一特性可将分汊区域或多连域分割成多个单连域分别进行求解,使几何图形复杂的计算区域网格的生成得到简化。
2.
Through solving the Laplace equations about physics co ordinate to transform plane,a numerical method of determining the grid points had been successfully used to generate the orthogonal co ordinate system.
采用物理坐标在变换平面求解拉普拉斯方程的方法生成正交坐标系 ,提出了双连通域的边界条件的处理及其数值计算过程 。
5) p-Laplace equation


p-拉普拉斯方程
1.
The existence of the solution for a singular p-Laplace equation involving critical Sobolev-Hardy exponent is studied: -div〔(|▽u|p-2▽u)/|x|β 〕=(up*-1)/|x|α+λuq-1,inΩ;u=0,onΩ by using Sobolev—Hardy inequality,Concentration Compactness Principle and the Mountain Pass Geometry.
利用Sobolev-Hardy不等式、集中紧原理、山路几何给出关于Sobolev-Hardy指数的含奇性p-拉普拉斯方程:-div〔(|▽u|p-2▽u)/|x|β〕=(up*-1)/|x|α+λuq-1,inΩ;u=0,on
6) laplacian equation


拉普拉斯方程
1.
In this paper a sufficient condition for mixed finite element space of lowest order for Laplacian Equation is derived and a new interpolation operator is constructed.
本文对拉普拉斯方程的最低次混合元方法提出了构造混合元空间的充分条件,并建立了新的插值算子。
补充资料:拉普拉斯方程
| 拉普拉斯方程 Laplace's equation 以法国P.-S.拉普拉斯命名的二阶偏微分方程。在三维直角坐标系中,它的形式是: 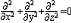 它的二次连续可微解称为调和函数,调和函数有极多的光滑性。拉普拉斯方程在物理吸广泛应用,因为它的解出现在电、磁、引力位势、稳态温度以及流体动力学各方面的问题中。 它的二次连续可微解称为调和函数,调和函数有极多的光滑性。拉普拉斯方程在物理吸广泛应用,因为它的解出现在电、磁、引力位势、稳态温度以及流体动力学各方面的问题中。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条