|
|
|
说明:双击或选中下面任意单词,将显示该词的音标、读音、翻译等;选中中文或多个词,将显示翻译。
|
|
|
1) test of rectangular plate

矩形薄板试验
2) thin rectangular plate

矩形薄板
1.
Interaction analysis between thin rectangular plate and elastic foundation;

矩形薄板与弹性半空间地基相互作用研究
2.
Primary parametric resonance of thin rectangular plate on nonlinear elastic foundation;

非线性弹性地基上矩形薄板的主参数共振
3.
Stochastic stability and bifurcation for a thin rectangular plate subject to in-plane stochastic parametrical excitation
矩形薄板在面内随机参数激励下的随机稳定性与分岔研究
3) rectangular thin plate

矩形薄板
1.
Free vibration of rectangular thin plate on elastic foundation with four edges free;

弹性地基上四边自由矩形薄板的自由振动
2.
Vibraitons of rectangular thin plates on Winkler′s foundation;

文克尔地基上矩形薄板的振动
3.
Exact solution of rectangular thin plate on vlazov elastic foundation with four edges free
双参数弹性地基上四边自由矩形薄板精确解
4) rectangular plate

矩形薄板
1.
Thermal buckling about reinforced concrete rectangular plate on elastic subgrade;

弹性地基上钢筋混凝土矩形薄板的热屈曲
2.
Based on the rigidity plate and the small deflection theories, and considering the physical nonlinearity of concrete, the equilibrium and stability equations of reinforced concrete rectangular plate subjected to thermal loading are derived.
基于刚性板和小挠度理论,考虑混凝土的材料非线性,推导了热载作用下钢筋混凝土矩形薄板的平衡方程和稳定方程。
3.
The closed form solution of the critical buckling temperature for a simply supported rectangular plate made of reinforced concrete under uniform heat variation were presented,and the influences of material constant,length-breadth ratio,relat.
基于板的小挠度理论,考虑混凝土材料的非线性,推导了弹性地基上钢筋混凝土矩形薄板在热载作用下的平衡方程和稳定方程,给出了四边简支钢筋混凝土矩形薄板在均匀温度变化时临界屈曲温度变化的封闭解,讨论了板的材料常数、长宽比、相对厚度和基床系数等对临界屈曲温度变化的影响,从而为工程结构中弹性地基上钢筋混凝土矩形薄板的临界屈曲温度的计算提供了理论计算依据。
5) Thin rectangular plates

矩形薄板
1.
Lewis method, solves bending problems Of thin rectangular plates with two simple supports and one of two free sides under uniform load, and its results provide a solid theoretical basis for the design of the plates.
Levy方法,解决了两对边简支、两自由边之一受均布载荷的矩形薄板的弯曲问题。
2.
The reciprocal method is applied to establish the generalized displacement solution for the elastic stability of thin rectangular plates, and the boundary values of it are also worked out.
本文引入了稳定问题的广义支承边和广义支承边矩形板的概念,应用功的互等法建立了弹性矩形薄板稳定问题的广义位移解,并给出了广义位移解的各个边界值。
6) elastic rectangular thin plate

弹性矩形薄板
1.
Solute elastic rectangular thin plate by symplectic geometry method;

求解弹性矩形薄板问题的辛几何法
2.
The analytical solutions for an elastic rectangular thin plate with two adjacent boundaries clamped-supported and the others simplified-supported are derived by a symplectic geometry method.
利用辛几何的方法推导出了两邻边固支另两邻边简支弹性矩形薄板问题的理论解。
3.
In this paper,the analytical solutions for an elastic rectangular thin plate with opposite boundary completely clamped support and others free were derived by a Symplectic geometry method.
利用辛几何的方法推导出了两对边固支另两对边自由支承条件情况下,弹性矩形薄板问题的理论解。
补充资料:矩形
一.型态分析 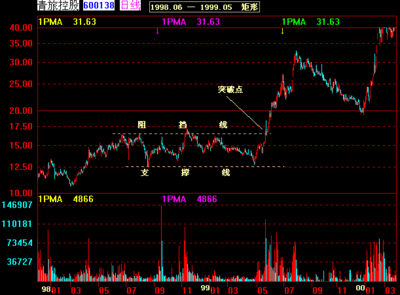
矩形是股价由一连串在二条水平的上下界线之间变动而成的型态。股价在其范围之内出现上落。价格上升到某水平时遇上阻力,掉头回落,但很快地便获得支持而升,可是回升到上次同一高点时再一次受阻,而挫落到上次低点时则再得到支持。这些短期高点和低点分别以直线连接起来,便可以绘出一条通道,这通道既非上倾,亦非下降,而是平行发展,这就是矩形型态。 [编辑] 二.市场含义 矩形为冲突型,是描述实力相当的争战双方的竞争。 这型态明显告诉我们,好淡双方的力量在该范围之间完全达致均衡状态,在这段期间谁占不了谁的便宜。看好的一方认为其价位是很理想的买入点,于是股价每回落到该水平即买入,形成了一条水平的需求线。与此同时,另一批看淡的投资者对股市没有信心,认为股价难以升越其水平,于是股价回升至该价位水平,便即沽售,形成一条平行的供给线。从另一个角度分析,矩形也可能是投资者因后市发展不明朗,投资态度变得迷惘和不知所措而造成。所以,当股价回升时,一批对后市缺乏信心的投资者退出;而当股价回落时,一批憧憬着未来前景的投资者加进,由于双方实力相若,于是股价就来回在这一段区域内波动。 一般来说,矩形是整理形态,市道牛皮上落,顺升市和跌市中都可能出现,长而窄且成交量小的矩形在原始底部比较常出现。突破上下了限后有买入和卖出的讯号,涨跌幅度通常等于矩形本身宽度。 [编辑] 三.要点提示 (1)矩形形成的过程中,除非有突发性的消息扰乱,其成交量应该是不断减少的。如果在型态形成期间,有不规则的高成交出现,型态可能失败。当股价突破矩形上限的水平时,必须有成交量激增的配合;但若跌破下限水平时,就不须高成交量的增加。 (2)矩形呈现突破后,股价经常出现反抽,这种情形通常会在突破后的三天至三星期内出现。反抽将止于顶线水平之上,往下跌破后的假性回升,将受阻于底线水平之下。 (3)一个高,低波幅较大的矩形,较一个狭窄而长的矩形型态更具威力。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|












