|
|
|
说明:双击或选中下面任意单词,将显示该词的音标、读音、翻译等;选中中文或多个词,将显示翻译。
|
|
|
1) rectangular thin cantilever plate

矩形悬臂薄板
1.
Fourier analysis of bending of orthogonal anisotropic rectangular thin cantilever plate

正交各向异性矩形悬臂薄板弯曲的傅立叶分析
2) rectangular cantilever plate

矩形悬臂板
1.
The bending Of a rectangular cantilever plate is a very complicated problem in the theory of Kirchhoff plate.
矩形悬臂板弯曲问题是Kirchhoff板理论中的难题。
2.
The analytical solution for bending of orthotropic rectangular cantilever plates is investigated by use of Stockes transformation of double variable function.
本文利用双变量函数Stockes变换研究正交各向异性矩形悬臂板的解析解。
3) cantilever rectangular plate

悬臂矩形板
1.
This paper emphasis to diacuss non-symmetric bending of cantilever rectangular plate support concentrated force on arbitrary point.
利用叠加原理及广义简支边的概念,着重讨论了悬臂矩形板在任意一点承受集中力作用的不对称弯曲。
2.
Taking the polynomial and trigonometric function as flexural funciton,the paper analyses the problem of the bending of orthotropic cantilever rectangular plate according to Rayleigh-Ritz method of the theory elasticity.
构造多项式和三角函数的混合形式作为挠度试函数 ,用Rayleigh -Ritz法求解了正交异性悬臂矩形板的弯曲问题。
3.
Finally,this proposed method is applied to designing the optimal locations for measuring the asymmetric bending deformation of a cantilever rectangular plate.
应用该方法对悬臂矩形板弯曲变形实测进行了测点优化布置,组合优化数值结果验证了该方法的可行性和有效性。
4) thin cantilever strip-plate

条形悬臂薄板
5) thin cantilever semicircular plate

悬臂半圆形薄板
6) rectangular cantilever thick plate

矩形悬臂厚板
1.
In this paper,the flexuous function w(x,y)and stress function Ψ(x,y)are selected,which consist of the trigonometrical series and polynomial expression,and the linear algebraic equa-tions are obtained solvable for rectangular cantilever thick plates under uniform surface-load.
选取由三角级数和多项式组成的挠度函数 w(x,y)和应力函数ψ(x,y),得到求解在均布荷载作用下,矩形悬臂厚板的线性代数方程组。
2.
A theoretic solution for rectangular cantilever thick plate is derived by symplectic geometry method.
首先把胡海昌提出的弹性厚板弯曲问题的简化方程表示成为Hamilton正则方程,然后利用辛几何方法对全状态相变量进行分离变量,求出其本征值后,再按本征函数展开的方法求出矩形悬臂厚板的解析解。
补充资料:矩形
一.型态分析 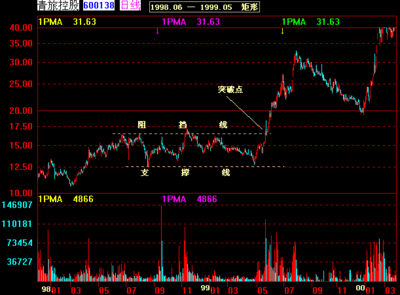
矩形是股价由一连串在二条水平的上下界线之间变动而成的型态。股价在其范围之内出现上落。价格上升到某水平时遇上阻力,掉头回落,但很快地便获得支持而升,可是回升到上次同一高点时再一次受阻,而挫落到上次低点时则再得到支持。这些短期高点和低点分别以直线连接起来,便可以绘出一条通道,这通道既非上倾,亦非下降,而是平行发展,这就是矩形型态。 [编辑] 二.市场含义 矩形为冲突型,是描述实力相当的争战双方的竞争。 这型态明显告诉我们,好淡双方的力量在该范围之间完全达致均衡状态,在这段期间谁占不了谁的便宜。看好的一方认为其价位是很理想的买入点,于是股价每回落到该水平即买入,形成了一条水平的需求线。与此同时,另一批看淡的投资者对股市没有信心,认为股价难以升越其水平,于是股价回升至该价位水平,便即沽售,形成一条平行的供给线。从另一个角度分析,矩形也可能是投资者因后市发展不明朗,投资态度变得迷惘和不知所措而造成。所以,当股价回升时,一批对后市缺乏信心的投资者退出;而当股价回落时,一批憧憬着未来前景的投资者加进,由于双方实力相若,于是股价就来回在这一段区域内波动。 一般来说,矩形是整理形态,市道牛皮上落,顺升市和跌市中都可能出现,长而窄且成交量小的矩形在原始底部比较常出现。突破上下了限后有买入和卖出的讯号,涨跌幅度通常等于矩形本身宽度。 [编辑] 三.要点提示 (1)矩形形成的过程中,除非有突发性的消息扰乱,其成交量应该是不断减少的。如果在型态形成期间,有不规则的高成交出现,型态可能失败。当股价突破矩形上限的水平时,必须有成交量激增的配合;但若跌破下限水平时,就不须高成交量的增加。 (2)矩形呈现突破后,股价经常出现反抽,这种情形通常会在突破后的三天至三星期内出现。反抽将止于顶线水平之上,往下跌破后的假性回升,将受阻于底线水平之下。 (3)一个高,低波幅较大的矩形,较一个狭窄而长的矩形型态更具威力。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|







