2) Generalization Yang Hui Triangle


杨辉三角的推广
3) Yang Hui triangle


杨辉三角形
1.
The properties of n-ary Yang Hui triangle and their applications in studying fixed-weight codeset matrix are also introduced.
本文提出多元杨辉三角形的概念。
2.
Through repeating the line of Yang Hui triangle,a new factional type can be got and the "fibonacci sequence" in defect of first term 1 in it can be discovered.
通过重置杨辉三角形的列,可得其派生型。
4) generalized Yanghui's triangle matrix


广义杨辉三角阵
5) the broad YangHui triangle


广义杨辉三角
1.
This paper introduced the construction and properties of the broad YangHui triangle,and discussed the relationship between the broad YangHui triangle and the power series of exponential e~x .
介绍了广义杨辉三角的构造、性质,以及它与指数函数ex的幂级数展开式的关系,继而讨论了它在配套概率方面的应用,最后得出有关广义杨辉三角更进一步的两个重要性质。
6) Order of Yanghui trangle


杨辉三角形排序
补充资料:杨辉三角形
| 杨辉三角形 Yang Hui triangle 由二项展开式的系数所排成的三角形。又称贾宪三角形,如下表:  表中第n行的n个数依次与二项展开式 表中第n行的n个数依次与二项展开式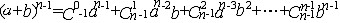 的几个系 的几个系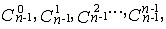 相等。从表上看,除1以外,每个数都等于它两肩上的两个数的和。 相等。从表上看,除1以外,每个数都等于它两肩上的两个数的和。杨辉三角形是中国北宋数学家贾宪(约1050年)首先发现的。南宋数学家杨辉在《详解九章算法》(1261年)一书中对此曾有记载。法国数学家B.帕斯卡在1654年也发现这个三角,故西方称之为帕斯卡三角形。按最早发现的时间,实应称贾宪三角形。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
