1) minimax solution of linear equations


线性方程组极值解
6) linear systems solving method


线性方程组解法
补充资料:线性方程组
| 线性方程组 linear equations,system of 各个方程关于未知量均为一次的方程组。对线性方程组的研究,中国比欧洲至少早1500年,记载在公元初《九章算术》方程章中。n个未知量m个方程的线性方程组的一般形式为 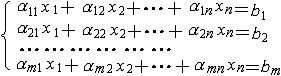 xj表未知量,aij称系数,bi称常数项。 xj表未知量,aij称系数,bi称常数项。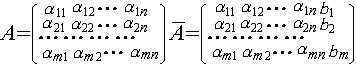 称为系数矩阵和增广矩阵。若x1=c1,x2=c2,…,xn=cn代入所给方程各式均成立,则称(c1,c2,…,cn)为一个解。若c1,c2,…,cn不全为0,则称(c1,c2,…,cn)为非零解。若常数项均为0,则称为齐次线性方程组,它总有零解(0,0,…,0)。两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组。线性方程组主要讨论的问题是:①一个方程组何时有解。②有解方程组解的个数。③对有解方程组求解,并决定解的结构。这几个问题均得到完满解决:所给方程组有解 称为系数矩阵和增广矩阵。若x1=c1,x2=c2,…,xn=cn代入所给方程各式均成立,则称(c1,c2,…,cn)为一个解。若c1,c2,…,cn不全为0,则称(c1,c2,…,cn)为非零解。若常数项均为0,则称为齐次线性方程组,它总有零解(0,0,…,0)。两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组。线性方程组主要讨论的问题是:①一个方程组何时有解。②有解方程组解的个数。③对有解方程组求解,并决定解的结构。这几个问题均得到完满解决:所给方程组有解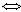 秩(A)=秩 秩(A)=秩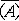 ;若秩(A)=秩 ;若秩(A)=秩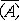 =r,则r=n时,有唯一解;r<n时,有无穷多解;可用消元法求解。克莱姆法则(见行列式)给出了一类特殊线性方程组解的公式。n个未知量的任一齐次方程组的解集均构成n维空间的一个子空间。 =r,则r=n时,有唯一解;r<n时,有无穷多解;可用消元法求解。克莱姆法则(见行列式)给出了一类特殊线性方程组解的公式。n个未知量的任一齐次方程组的解集均构成n维空间的一个子空间。线性方程组有广泛应用,熟知的线性规划问题即讨论对解有一定约束条件的线性方程组问题。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条