1) linear equations


线性方程组
1.
A parallel Guass-Seidel iterative algorithm for solving linear equations on LAN;


一种网上求解线性方程组的Guass-Seidel并行迭代算法
2.
Analyze on the methods of solution for linear equations;


分析有限元线性方程组的求解方法
3.
New methods for finding the solution to linear equations;


线性方程组求解的新方法
2) system of linear equations


线性方程组
1.
Some iteration formula and error estimate of system of linear equations;


线性方程组迭代解法的补充定理
2.
The Adomaint theory and the computing of system of linear equations on LAN;


Adomaint原理与线性方程组的网络并行计算
3.
A simple exploration on structure of solutions of system of linear equations;


线性方程组解的结构探讨
3) linear systems


线性方程组
1.
We find out an upper bound of R_1-factor of two-stage iterative methods for solution of linear systems.
给出了线性方程组二级迭代法R1-收敛因子的一个上界,这个上界由内、外迭代的R1-收敛因子和内迭代次数所决定,其主部为外迭代的R1-收敛因子。
2.
In this paper, the necessary and sufficient conditions for such special linear systems having solutions and unique solution is studied, and the conditions are expressed by A?B?D?f and g.
在许多领域中 ,常需要解下列形状的线性方程组ABTB -Dxy =fg其中 ,A ∈Rn×n,B ∈Rm×n,D ∈Rm×m ,且A、D对称非负定。
3.
Solving large scale matrix problems including large linear systems, eigenvalue problems, etc.
求解大规模矩阵问题包括线性方程组和特征值问题等是计算数学和科学工程计算中的重大课题。
4) linear equation group


线性方程组
1.
The solution of the linear equation group can be thought as the intersection of all the hyper-planes which represent the group basing on the analytic geometry.
由解析几何观点知道,线性方程组解的几何意义是方程组中各个方程所代表的超平面的交点。
2.
The existence and uniqueness of the solution to matrix equation AX+XB=C are discussed according to the method of solving linear equation group, and a group of linear equation groups are established, based on which solution to AX+XB=C can be obtained easily.
针对矩阵方程 AX+XB=C的求解问题,利用解标准的线性方程组方法讨论了该矩阵方程解的存在性和惟一性,并将其变换成一组简单的线性方程组,在此基础上可方便地求出该矩阵方程的解。
3.
The method of solving the linear programming is introduced by using Excel,then the method is extended to solve maths problems such as inequality and linear equation group.
介绍了用Excel软件求解线性规划的方法,在此基础上给出了用该软件求解不等式问题和线性方程组的方法。
5) linear equation


线性方程组
1.
Solving linear equations by elementary column transformations;


用列初等变换求解线性方程组
2.
To solve linear equation using matrix elementary columu vary;


利用矩阵的初等列变换解非齐次线性方程组
3.
The solution-set s structure for inverse problem of system of linear equation Ax=b;


线性方程组Ax=b的反问题解集的构造
6) linear system of equations


线性方程组
1.
An all-purpose algorithm for solving linear and nonlinear system of equations;


求解线性和非线性方程组的一种通用算法
2.
Transform the original linear system of equations into an optimization problem of its equivalent variational problem.
把线性方程组转化成为其等价的变分问题 ,借助黄金分割法的思想对该变分问题进行求解 ,给出的算例结果表明 ,本文方法不仅对良态线性方程组的求解有效 ,而且对于病态线性方程组的求解同样是有效实用的 。
补充资料:线性方程组
| 线性方程组 linear equations,system of 各个方程关于未知量均为一次的方程组。对线性方程组的研究,中国比欧洲至少早1500年,记载在公元初《九章算术》方程章中。n个未知量m个方程的线性方程组的一般形式为 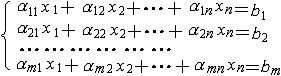 xj表未知量,aij称系数,bi称常数项。 xj表未知量,aij称系数,bi称常数项。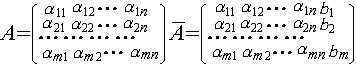 称为系数矩阵和增广矩阵。若x1=c1,x2=c2,…,xn=cn代入所给方程各式均成立,则称(c1,c2,…,cn)为一个解。若c1,c2,…,cn不全为0,则称(c1,c2,…,cn)为非零解。若常数项均为0,则称为齐次线性方程组,它总有零解(0,0,…,0)。两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组。线性方程组主要讨论的问题是:①一个方程组何时有解。②有解方程组解的个数。③对有解方程组求解,并决定解的结构。这几个问题均得到完满解决:所给方程组有解 称为系数矩阵和增广矩阵。若x1=c1,x2=c2,…,xn=cn代入所给方程各式均成立,则称(c1,c2,…,cn)为一个解。若c1,c2,…,cn不全为0,则称(c1,c2,…,cn)为非零解。若常数项均为0,则称为齐次线性方程组,它总有零解(0,0,…,0)。两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组。线性方程组主要讨论的问题是:①一个方程组何时有解。②有解方程组解的个数。③对有解方程组求解,并决定解的结构。这几个问题均得到完满解决:所给方程组有解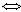 秩(A)=秩 秩(A)=秩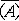 ;若秩(A)=秩 ;若秩(A)=秩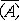 =r,则r=n时,有唯一解;r<n时,有无穷多解;可用消元法求解。克莱姆法则(见行列式)给出了一类特殊线性方程组解的公式。n个未知量的任一齐次方程组的解集均构成n维空间的一个子空间。 =r,则r=n时,有唯一解;r<n时,有无穷多解;可用消元法求解。克莱姆法则(见行列式)给出了一类特殊线性方程组解的公式。n个未知量的任一齐次方程组的解集均构成n维空间的一个子空间。线性方程组有广泛应用,熟知的线性规划问题即讨论对解有一定约束条件的线性方程组问题。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条